Система координат Antenna Toolbox

В Antenna Toolbox™ используются два типа системы координат: прямоугольная система координат и сферическая система координат.

Antenna Toolbox использует прямоугольную систему координат, чтобы визуализировать геометрию антенны или массива. Тулбокс использует сферическую систему координат, чтобы визуализировать диаграммы направленности антенного излучения.

Прямоугольная система координат

Визуализируйте геометрию monopoleTopHat по умолчанию антенна из библиотеки антенн.

m = monopoleTopHat;
show(m);

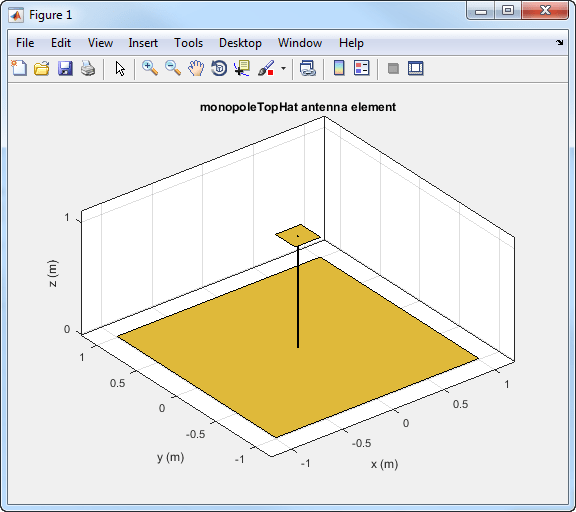
Тулбокс отображает антенну верхнего монополя в прямоугольной или декартовой системе координат.

Прямоугольная система координат, также называемая Декартовой системой координат, задает положение в пространстве как упорядоченный 3-кортеж вещественных чисел (x,y,z), относительно origin (0,0,0).

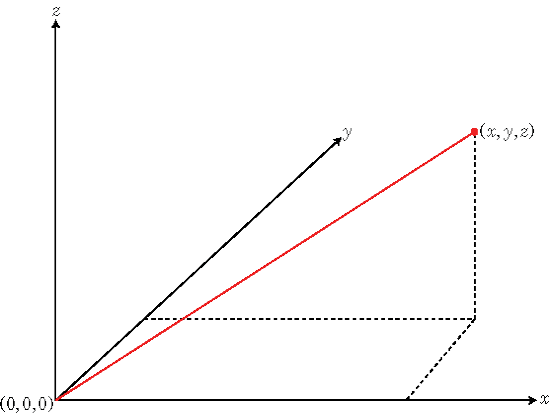
Можно просмотреть 3-кортеж как точку в пространстве или эквивалентно как вектор в трехмерном евклидовом пространстве. При рассмотрении как вектора в пространстве координатные оси являются базисными векторами, и вектор задает направление в точку пространства от источника. Каждый вектор в пространстве однозначно определяется линейной комбинацией базисных векторов. Наиболее распространенным набором базисных векторов для трехмерного евклидова пространства являются стандартные единичные базисные векторы:

${[1 0 0], [0 1 0], [0 0 1]}$

Ортогональный базис и евклидова норма

Любые три линейно независимых векторы задают базис для 3-мерного пространства. Однако Antenna Toolbox принимает, что используемые вами базисные векторы ортогональны.

Стандартной мерой расстояния в пространстве является l² норма, или евклидова норма. Евклидова норма вектора [x y z] определяется:

$\sqrt{x^{2} + y^{2} + z^{2}}$

Евклидова норма задает длину вектора, измеренную от источника, как гипотенузу прямоугольного треугольника. Расстояние между двумя векторами [x0 y0 z0] и [x1 y1 z1] составляет:

$\sqrt{{(x_{0} - x_{1})}^{2} + {(y_{0} - y_{1})}^{2} + {(z_{0} - z_{1})}^{2}}$

Сферическая система координат

Визуализируйте диаграмму направленности излучения по умолчанию monopoleTopHat антенна.

m = monopoleTopHat;
pattern(m,75e6);

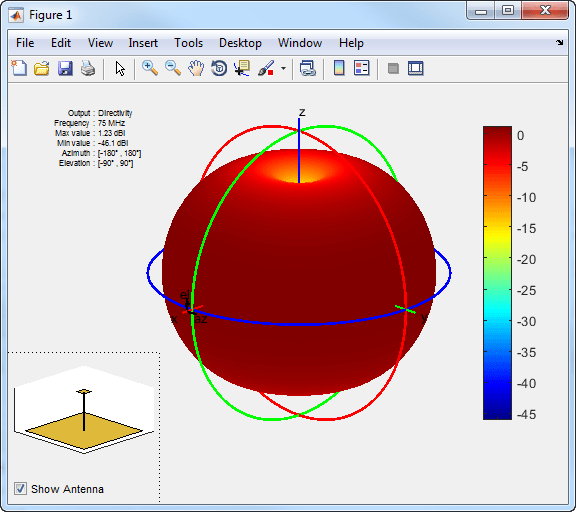
Тулбокс отображает диаграмму направленности излучения монополя верхней шляпы, используя сферическую систему координат, представленную азимутом и углами возвышения.

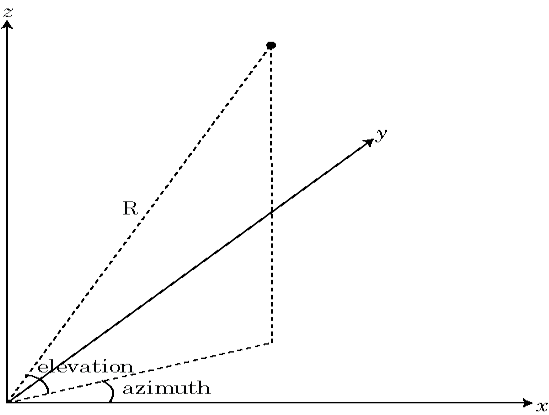
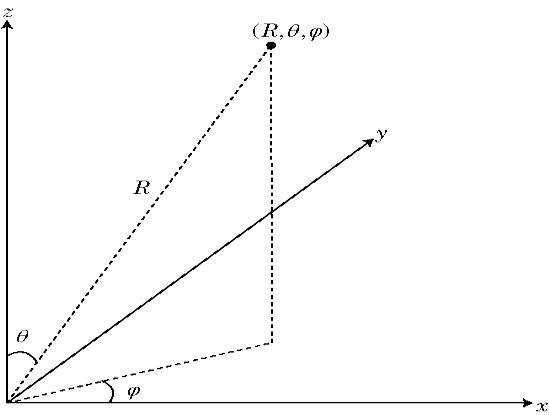
Сферическая система координат задает вектор или точку в пространстве с расстоянием R и двумя углами. Можно представлять углы в этой системе координат:

Азимут и углы возвышения
Углы Phi (В) и theta (В)
u и v координат

Азимут и углы возвышения

Угол азимута является углом от положительной оси X до ортогональной проекции вектора на плоскость xy, движущуюся в направлении к оси Y. Угол азимута находится в области значений -180 и 180 степеней.

Угол возвышения является углом от ортогональной проекции вектора на плоскости xy к положительной оси Z к вектору. Размер угла возвышения составляет -90 и 90 степени.

Углы Phi (В) и Theta (В)

Угол и есть угол от положительной оси X до ортогональной проекции вектора на плоскость xy, движущуюся в направлении к оси Y. Угол азимута находится между -180 и 180 степенями.

Угол и есть угол от положительной оси z до самого вектора. Угол и угол находятся в области значений 0 степеней и 180 степеней.

Эти углы являются альтернативой использованию азимута и углов возвышения для выражения местоположения точки в сферу единичного радиуса.

u и v координаты

Можно задать u и v в терминах

$\begin{array}{l} u = \sin θ \cos ϕ \\ v = \sin θ \sin ϕ \end{array}$

С точки зрения азимута и углов возвышения координаты u и v:

$\begin{array}{l} u = \cos e l \sin a z \\ v = \sin e l \end{array}$

Значения u и v удовлетворяют неравенствам:

$\begin{array}{l} - 1 \leq u \leq 1 \\ - 1 \leq v \leq 1 \\ u^{2} + v^{2} \leq 1 \end{array}$

В терминах u и v углы

$\begin{array}{l} \tan ϕ = u / v \\ \sin θ = \sqrt{u^{2} + v^{2}} \end{array}$

Азимут и углы возвышения в терминах u и v:

$\begin{array}{l} \sin e l = v \\ \tan a z = \frac{u}{\sqrt{1 - u^{2} - v^{2}}} \end{array}$

Преобразование между прямоугольной и сферической координатами

Преобразуйте прямоугольные координаты в сферические координаты (az, el, R) с помощью:

$\begin{array}{l} R = \sqrt{x^{2} + y^{2} + z^{2}} \\ a z = \tan^{- 1} (\frac{y}{x}) \\ e l = \tan {}^{- 1}{(\frac{z}{\sqrt{x^{2} + y^{2}}})} \end{array}$

Преобразуйте сферические координаты (az, el, R) в прямоугольные с помощью:

$\begin{array}{l} x = R \cos (e l) \cos (a z) \\ y = R \cos (e l) \sin (a z) \\ z = R \sin (e l) \end{array}$

где:

R - расстояние от антенны
el и az - азимут и углы возвышения

Ссылки

[1] Balanis, C.A. Antenna Theory: Analysis and Design. 3rd Ed. New York: Wiley, 2005.

Документация