Модулируйте с использованием однополосной амплитудной модуляции
Аналоговая модуляция полосы пропускания, в модуляции
Блок SSB AM Modulator Passband модулирует использование однополосной амплитудной модуляции с фильтром преобразования Гильберта. Выход является представлением полосы пропускания модулированного сигнала. И вход, и выход сигналы являются сигналами реального скаляра.
SSB AM Modulator Passband передает сигнал либо нижней, либо верхней боковой полосы, но не обеих. Чтобы контролировать, какую боковую полосу она передает, используйте параметр Sideband to modulate.
Если вход u (t) как функция от временных t, то выход
где:
f c является параметром Carrier frequency.
.r- Initial phase параметр.
û (t) является преобразованием Гильберта входного u (t).
Знак минус указывает на верхнюю боковую полосу, а знак плюс - на нижнюю боковую полосу.
Этот блок использует Analytic Signal блок из библиотеки блоков DSP System Toolbox™ Transforms.
Блок Analytic Signal вычисляет комплексный аналитический сигнал, соответствующий каждому каналу действительного M-на-N входа u
где и обозначает преобразование Гильберта. Действительная часть выхода в каждом канале является репликой действительного входа в этом канале; мнимая часть является преобразованием Гильберта входа. В частотный диапазон аналитический сигнал сохраняет положительное частотное содержимое исходного сигнала при обнулении отрицательных частот и удвоении компонента постоянного тока.
Блок вычисляет преобразование Гильберта с помощью конечной импульсной характеристики фильтра equiripple с порядком, заданным параметром порядка Фильтра, n. Линейный фильтр фазы разработан с помощью алгоритма Remez exchange и накладывает задержку n/2 на вход выборки.
Для наилучших результатов используйте несущую частоту, которая, по оценкам, превышает 10% от частоты дискретизации вашего входного сигнала. Это связано с реализацией преобразования Гильберта с помощью фильтра.
В следующем примере мы дискретизируем 10Hz входной сигнал со скоростью 8000 выборок в секунду. Затем обозначим Преобразование Гильберта фильтр порядка 100. Ниже приведена реакция Преобразования Гильберта фильтра, возвращенная fvtool.
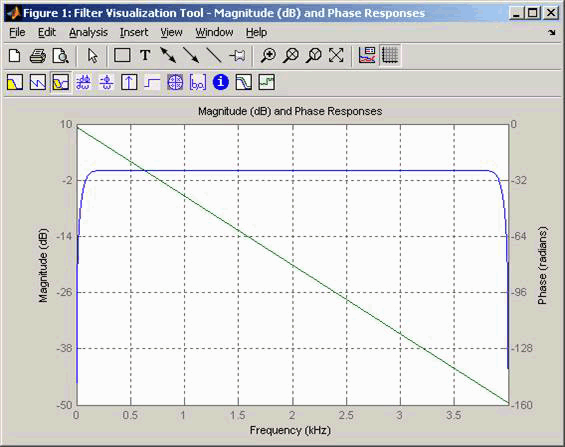
Обратите внимание на пропускную способность характеристики величины фильтра. Путем выбора несущей частоты более 10% (но менее 90%) Шаг расчета входного сигнала (8000 выборки в секунду, в этом примере) или, что эквивалентно, несущая частота, больше 400Hz, мы гарантируем, что фильтр преобразования Гильберта будет работать в плоской части величины характеристики фильтра (показан синим цветом), и что наш модулированный сигнал будет иметь желаемую величину и форму.
Обычно соответствующее Carrier frequency значение намного выше, чем самая высокая частота входного сигнала. По теореме Найквиста о дискретизации, взаимное значение шага расчета модели (заданное источником сигнала модели) должно превысить в два раза Carrier frequency параметр.
Этот блок работает только с действительными входами типа double. Этот блок не работает внутри триггируемой подсистемы.
Частота несущей.
Смещение фазы, , модулированного сигнала.
Этот параметр определяет, передавать ли верхнюю или нижнюю боковую полосу.
Длина конечной импульсной характеристики, используемого для вычисления преобразования Гильберта.
[1] Peebles, Peyton Z, Jr. Принципы коммуникационной системы. Чтение, месса.: Эддисон-Уэсли, 1976.