Скалярное квантование является процессом, который преобразует все входы в заданную область в общее значение. Этот процесс преобразует входы в другой области значений значений в другое общее значение. В эффект скалярное квантование оцифровывает аналоговый сигнал. Квантование определяют два параметра: раздел и кодовая книга.
Разбиение квантования задает несколько смежных, непересекающиеся области значений значений в наборе вещественных чисел. Чтобы задать раздел в MATLAB® окружение, перечислите различные конечные точки различных областей значений в векторе.
Например, если раздел разделяет действительную числовую линию на четыре набора
{x: x ≤ 0}
{x: 0 < x ≤ 1}
{x: 1 < x ≤ 3}
{x: 3 < x}
тогда можно представлять разбиение как трехэлементный вектор
partition = [0,1,3];
Длина вектора разбиения на один меньше, чем количество интервалов разбиения.
Кодовая книга сообщает квантователю, какое общее значение следует присвоить входам, которые попадают в каждую область значений раздела. Представьте кодовую книгу как вектор, чья длина совпадает с количеством интервалов разбиения. Для примера, вектор
codebook = [-1, 0.5, 2, 3];
является одной возможной кодовой книгой для раздела [0,1,3].
quantiz функция также возвращает вектор, который сообщает, в каком интервале находится каждый вход. Для примера в выход ниже сказано, что значения входа находятся в пределах интервалов, обозначенных 0, 6 и 5, соответственно. Здесь 0-й интервал состоит из вещественных чисел, меньших или равных 3; 6-й интервал состоит из вещественных чисел больше 8, но меньше или равен 9; и 5-й интервал состоит из вещественных чисел, больше 7, но меньше или равно 8.
partition = [3,4,5,6,7,8,9]; index = quantiz([2 9 8],partition)
Это выход
index =
0
6
5
Если вы продолжаете этот пример, определяя вектор кодовой книги, такой как
codebook = [3,3,4,5,6,7,8,9];
затем приведенное ниже уравнение связывает вектор index к квантованному сигналу quants.
quants = codebook(index+1);
Эта формула для quants именно то, что quantiz function использует, если вместо этого описать пример более кратко, как показано ниже.
partition = [3,4,5,6,7,8,9]; codebook = [3,3,4,5,6,7,8,9]; [index,quants] = quantiz([2 9 8],partition,codebook);
Квантование искажает сигнал. Можно уменьшить искажения, выбрав соответствующие параметры разбиения и кодовой книги. Однако тестирование и выбор параметров для больших наборов сигналов с тонкой схемой квантования может быть утомительным. Одним из способов легкого создания параметров разделов и кодовых книг является их оптимизация в соответствии с набором так называемых обучающих данных.
Примечание
Обучающие данные, которые вы используете, должны быть типичными для видов сигналов, которые вы фактически будете квантовать.
lloyds функция оптимизирует раздел и кодовую книгу согласно алгоритму Ллойда. Приведенный ниже код оптимизирует разбиение и кодовую книгу для одного периода синусоидального сигнала, начиная с грубого начального предположения. Затем он использует эти параметры, чтобы квантовать исходный сигнал, используя начальные параметры догадки, а также оптимизированные параметры. Этот выход показывает, что среднее квадратное искажение после квантования намного меньше для оптимизированных параметров. quantiz функция автоматически вычисляет среднее квадратное искажение и возвращает его как третий выходной параметр.
% Start with the setup from 2nd example in "Quantizing a Signal." t = [0:.1:2*pi]; sig = sin(t); partition = [-1:.2:1]; codebook = [-1.2:.2:1]; % Now optimize, using codebook as an initial guess. [partition2,codebook2] = lloyds(sig,codebook); [index,quants,distor] = quantiz(sig,partition,codebook); [index2,quant2,distor2] = quantiz(sig,partition2,codebook2); % Compare mean square distortions from initial and optimized [distor, distor2] % parameters.
Это выход
ans =
0.0148 0.0024Код ниже показывает, как quantiz функция использует partition и codebook чтобы сопоставить вектор действительных чисел, samp, к новому вектору, quantized, записи которого: -1, 0,5, 2 или 3.
partition = [0,1,3]; codebook = [-1, 0.5, 2, 3]; samp = [-2.4, -1, -.2, 0, .2, 1, 1.2, 1.9, 2, 2.9, 3, 3.5, 5]; [index,quantized] = quantiz(samp,partition,codebook); quantized
Ниже приведен выход.
quantized =
Columns 1 through 6
-1.0000 -1.0000 -1.0000 -1.0000 0.5000 0.5000
Columns 7 through 12
2.0000 2.0000 2.0000 2.0000 2.0000 3.0000
Column 13
3.0000
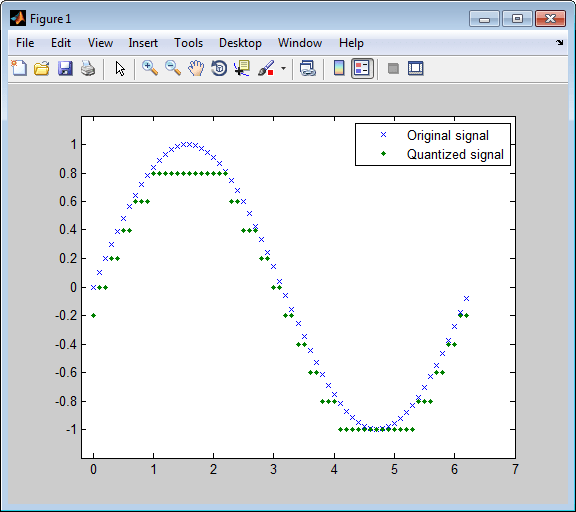
Этот пример более четко иллюстрирует природу скалярного квантования. После квантования дискретизированной синусоиды она строит графики исходных и квантованных сигналов. График контрастирует с xони составляют синусоидальную кривую с точками, которые составляют квантованный сигнал. Вертикальная координата каждой точки является значением в векторе codebook.
t = [0:.1:2*pi]; % Times at which to sample the sine function sig = sin(t); % Original signal, a sine wave partition = [-1:.2:1]; % Length 11, to represent 12 intervals codebook = [-1.2:.2:1]; % Length 12, one entry for each interval [index,quants] = quantiz(sig,partition,codebook); % Quantize. plot(t,sig,'x',t,quants,'.') legend('Original signal','Quantized signal'); axis([-.2 7 -1.2 1.2])