Нейроконтроллер, описанный в этом разделе, упоминается как два разных имен: управление линеаризацией с обратной связью и управление NARMA-L2. Он упоминается как линеаризация с обратной связью, когда модель объекта управления имеет конкретную форму (сопутствующую форму). Это называется управлением NARMA-L2 когда модель объекта управления может быть аппроксимирована той же формой. Центральная идея этого типа управления состоит в том, чтобы преобразовать динамику нелинейных систем в линейную динамику путем отмены нелинейностей. Этот раздел начинается с представления системной модели и демонстрации того, как вы можете использовать нейронную сеть для идентификации этой модели. Затем описывается, как идентифицированная модель нейронной сети может использоваться для разработки контроллера. Далее приводится пример использования блока NARMA-L2 Control, который содержится в blockset Deep Learning Toolbox™.
Как и в случае прогнозирующего управления моделью, первый шаг в использовании управления линеаризацией (или NARMA-L2) с обратной связью состоит в том, чтобы идентифицировать систему, которой будут управлять. Вы обучаете нейронную сеть, чтобы представлять прямую динамику системы. Первым шагом является выбор структуры модели для использования. Одной из стандартных моделей, которая используется для представления общих нелинейных систем дискретного времени, является нелинейная модель авторегрессивно-скользящего среднего значения (NARMA):
где u (k) - системный вход, а y (k) - системный выход. Для фазы идентификации можно обучить нейронную сеть аппроксимировать нелинейную функциональную N. Это процедура идентификации, используемая для NN-прогнозирующего контроллера.
Если вы хотите, чтобы выход следовал некоторой ссылочной траектории
y ( k + d ) = yr (k + d) следующим шагом является разработка нелинейного контроллера вида:
Проблема с использованием этого контроллера заключается в том, что, если вы хотите обучить нейронную сеть создавать G функции для минимизации средней квадратной ошибки, вам нужно использовать динамическое обратное распространение ([NaPa91] или [HaJe99]). Это может быть довольно медленно. Одним из решений, предложенных Narendra и Mukhopadhyay [NaMu97], является использование приблизительных моделей для представления системы. Контроллер, используемый в этом разделе, основан на NARMA-L2 приблизительной модели:
Эта модель находится в сопутствующей форме, где следующий входной u контроллера (k) не содержится внутри нелинейности. Преимущество этой формы в том, что вы можете решить для входа управления, который заставляет выход системы следовать ссылке y (k + d) = yr (k + d). Получившийся контроллер имел бы форму
Использование этого уравнения непосредственно может вызвать проблемы реализации, потому что вы должны определить входной u управления (k) на основе выхода одновременно, y (k). Итак, вместо этого используйте модель
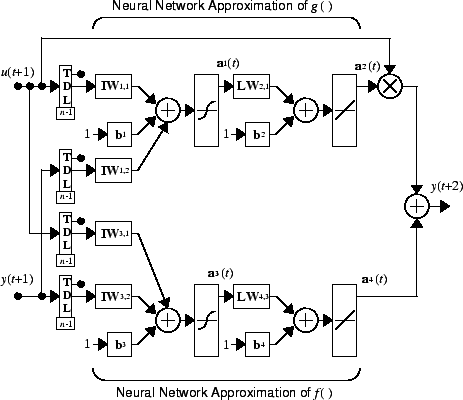
где d ≥ 2. Следующий рисунок показывает структуру представления нейронной сети.
Используя модель NARMA-L2, можно получить контроллер
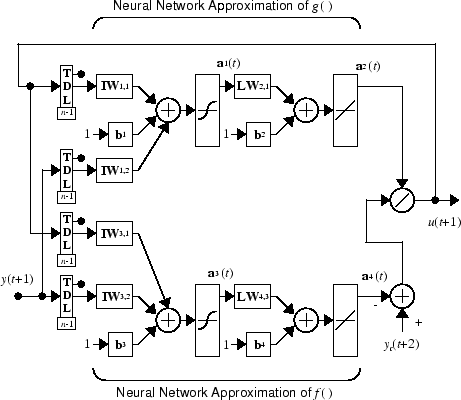
который реализуется для d ≥ 2. Следующий рисунок является блоком контроллера NARMA-L2.
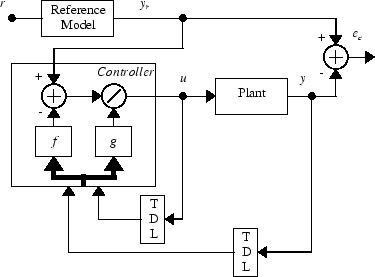
Этот контроллер может быть реализован с ранее идентифицированной NARMA-L2 моделью объекта управления, как показано на следующем рисунке.
В этом разделе показано, как обучен контроллер NARMA-L2. Первым шагом является копирование блока NARMA-L2 Controller из библиотеки блоков Deep Learning Toolbox в Simulink® Редактор. Смотрите документацию Simulink, если вы не уверены, как это сделать. Этот шаг пропущен в следующем примере.
Пример модели обеспечивается программным обеспечением Deep Learning Toolbox, чтобы показать использование контроллера NARMA-L2. В этом примере цель состоит в том, чтобы управлять положением магнита, подвешенного над электромагнитом, где магнит ограничен так, чтобы он мог двигаться только в вертикальном направлении, как на следующем рисунке.
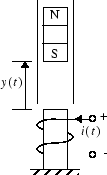
Уравнение движения для этой системы является
где y (t) - расстояние магнита над электромагнитом, i (t) - ток, протекающий в электромагните, M - масса магнита, а g - ускорение свободного падения. Параметр β является коэффициентом вязкого трения, который определяется материалом, в котором магнит движется, и α является константой напряженности поля, которая определяется количеством оборотов провода на электромагните и силой магнита.
Чтобы запустить этот пример:
Запуск MATLAB®.
Тип narmamaglev в Командном Окне MATLAB. Эта команда открывает Редактор Simulink со следующей моделью. Блок NARMA-L2 Control уже находится в модели.
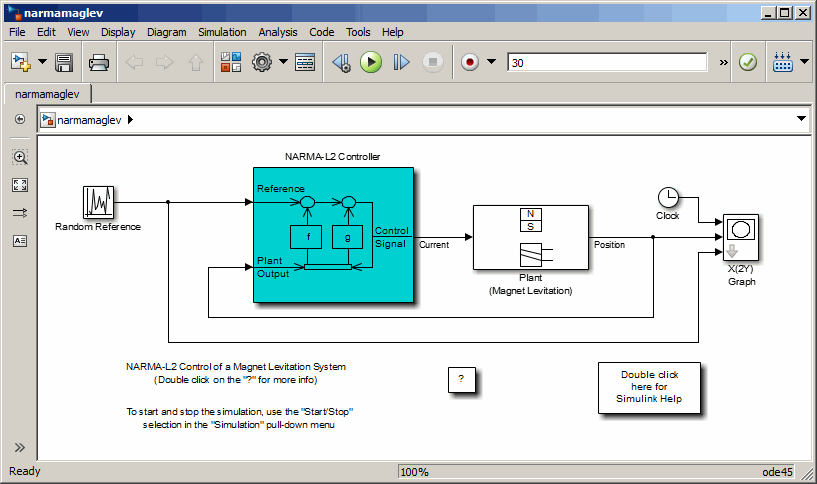
Дважды кликните блок NARMA-L2 Controller. Откроется следующее окно. Это окно позволяет вам обучить модель NARMA-L2. Отдельного окна для контроллера нет, потому что контроллер определяется непосредственно из модели, в отличие от прогнозирующего контроллера модели.
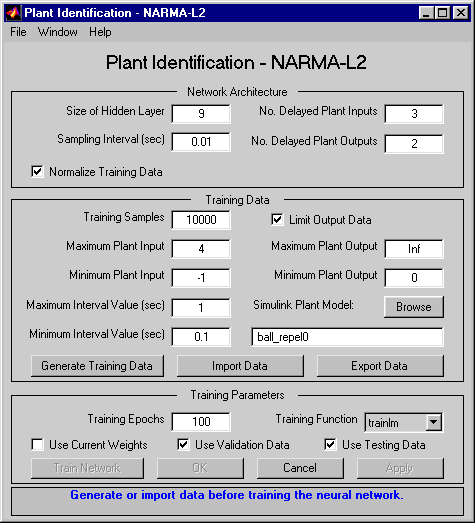
Это окно работает так же, как и другие окна идентификации объекта, поэтому процесс обучения не повторяется. Вместо этого моделируйте контроллер NARMA-L2.
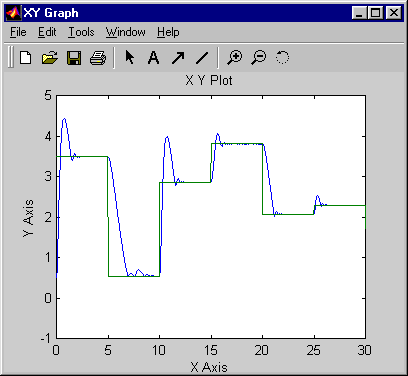
Вернитесь в Редактор Simulink и запустите симуляцию, выбрав опцию меню Simulation > Run. При выполнении моделирования отображаются выходы объекта и опорного сигнала, как показано на следующем рисунке.