Арифметика с фиксированной точкой

Сложение и вычитание

Сложение чисел с фиксированной точкой требует, чтобы двоичные точки дополнений были выровнены. Сложение затем выполняется с использованием двоичной арифметики, так что не используется никакое число, кроме 0 или 1.

Например, рассмотрите сложение 010010.1 (18.5) с 0110.110 (6.75):

$\begin{matrix} \begin{array}{r} \underline{\begin{matrix} 010010.1 \\ + 0110.110 \end{matrix}} \\ 011001.010 \end{array} & \begin{array}{l} (18.5) \\ (6.75) \\ (25.25) \end{array} \end{matrix}$

Вычитание с фиксированной точкой эквивалентно сложению при использовании значения дополнения двух для любых отрицательных значений. При вычитании дополнения должны быть расширены, чтобы соответствовать длине друг друга. Например, рассмотрите вычитание 0110.110 (6.75) из 010010.1 (18.5):

$\begin{matrix} \underline{\begin{matrix} 010010.100 \\ - 0110.110 \end{matrix}} & \begin{matrix} (18.5) \\ (6.75) \end{matrix} \end{matrix}$

Глобальный фимат по умолчанию имеет значение 1 (true) для CastBeforeSum свойство. Это приводит к добавлению типа суммарных данных перед сложением. Поэтому никакая дальнейшая перемена не требуется во время сложения, чтобы выровнять двоичные точки.

Если CastBeforeSum имеет значение 0 (false), добавляются дополнения с полной точностью. После сложения сумма квантуется.

Умножение

Умножение чисел с фиксированной точкой двух комплементов прямо аналогично регулярному десятичному умножению, за исключением того, что промежуточные результаты должны быть расширены знаком так, чтобы их левые стороны выровнялись, прежде чем вы сложите их вместе.

Для примера рассмотрим умножение 10,11 (-1,25) на 011 (3):

Типы данных умножения

Следующие схемы показывают типы данных, используемые для умножения с фиксированной точкой с помощью программного обеспечения Fixed-Point Designer™. Схемы иллюстрируют различия между типами данных, используемыми для реального, комплексно-реального и комплексно-комплексного умножения.

Реальное-реальное умножение. Следующая схема показывает типы данных, используемые тулбоксом в умножении двух вещественных чисел. Программное обеспечение возвращает выходы этой операции в типе данных продукта, который управляется fimath ProductMode объекта свойство.

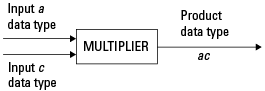
Умножение реального комплекса. Следующая схема показывает типы данных, используемые тулбоксом в умножении действительного и комплексного числа с фиксированной точкой. Действительное-комплексное и комплексно-действительное умножение эквивалентны. Программное обеспечение возвращает выходы этой операции в типе данных продукта, который управляется fimath ProductMode объекта свойство:

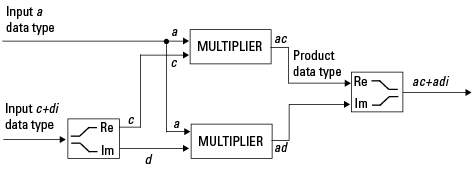
Комплексно-Комплексное Умножение. Следующая схема показывает умножение двух комплексных чисел с фиксированной точкой. Обратите внимание, что программное обеспечение возвращает выход этой операции в типе суммарных данных, который управляется fimath SumMode объекта свойство. Промежуточный тип данных продукта определяется fimath ProductMode объекта свойство.

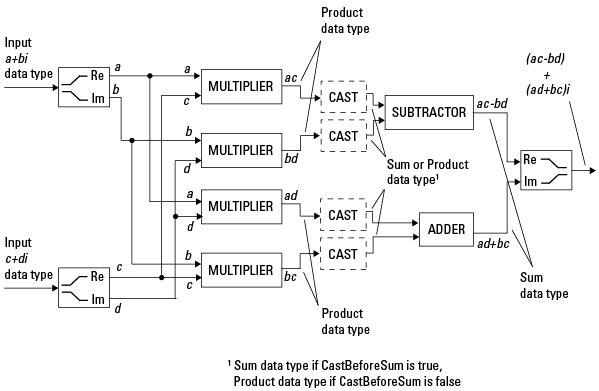
Когда fimath CastBeforeSum объекта свойство true, приведения к типу суммарных данных присутствуют после умножителей на предыдущей схеме. В коде С это эквивалентно

acc=ac;
acc-=bd;

для вычитателя, и

acc=ad;
acc+=bc;

для сумматора, где acc является аккумулятором. Когда CastBeforeSum свойство false, отливки не присутствуют, и данные остаются в типе данных продукта перед операциями вычитания и сложения.

Умножение с фиматом

В следующих примерах позвольте

F = fimath('ProductMode','FullPrecision',...
'SumMode','FullPrecision');
T1 = numerictype('WordLength',24,'FractionLength',20);
T2 = numerictype('WordLength',16,'FractionLength',10);

Real * Real . Заметьте, что размер слова и длина дроби результата z равны сумме размеров слова и дробей, соответственно, мультипликандов. Это потому, что fimath SumMode и ProductMode для свойств задано значение FullPrecision:

P = fipref;
P.FimathDisplay = 'none';
x = fi(5, T1, F) 

x =
 
     5


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10, T2, F) 

y =
 
    10


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y 

z =
 
    50


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

Реальный * комплекс . Заметьте, что размер слова и длина дроби результата z равны сумме размеров слова и дробей, соответственно, мультипликандов. Это потому, что fimath SumMode и ProductMode для свойств задано значение FullPrecision:

x = fi(5,T1,F) 

x =
 
     5


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20
 
y = fi(10+2i,T2,F) 

y =
 
  10.0000 + 2.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10
 
z = x*y 

z =
 
  50.0000 +10.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

Комплекс * Комплекс . Комплексно-комплексное умножение включает сложение, а также умножение, поэтому размер слова результата полной точности имеет на один бит больше, чем сумма размеров слова мультипликандов:

x = fi(5+6i,T1,F) 

x =
 
   5.0000 + 6.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20
 
y = fi(10+2i,T2,F) 

y =
 
  10.0000 + 2.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10
 
z = x*y 

z =
 
  38.0000 +70.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 41
        FractionLength: 30

Арифметика по модулю

Двоичная математика основана на арифметике по модулю. Модульная арифметика использует только конечное значение чисел, заворачивая результаты любых вычислений, которые попадают вне заданного множества назад во множество.

Для примера обычные повседневные часы используют арифметику по модулю 12. Номера в этой системе могут быть только от 1 до 12. Поэтому в «тактовой» системе 9 плюс 9 равен 6. Это может быть легче визуализировать как числовой круг:

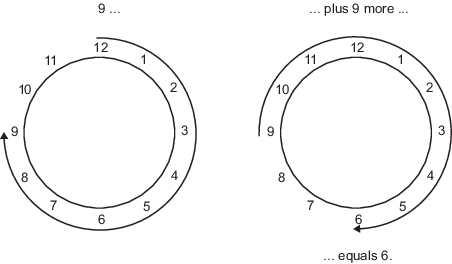
Точно так же двоичная математика может использовать только числа 0 и 1, и любые арифметические результаты, которые попадают за пределы этой области значений, оборачиваются «по кругу» в 0 или 1.

Дополнение двоих

Дополнение двух является способом интерпретации двоичного числа. В дополнении двух положительные числа всегда начинаются с 0, а отрицательные - с 1. Если начальный бит числа дополнения двойки равен 0, значение получается путем вычисления стандартного двоичного значения числа. Если начальный бит числа дополнения двойки равен 1, значение получается путем принятия, что самый левый бит отрицателен, и затем вычисления двоичного значения числа. Для примера,

$\begin{array}{l} 01 = (0 + 2^{0}) = 1 \\ 11 = ((- 2^{1}) + (2^{0})) = (- 2 + 1) = - 1 \end{array}$

Чтобы вычислить отрицательное значение двоичного числа с помощью дополнения двух,

Возьми свое дополнение или «переверни биты».
Добавьте 2 ^ (- FL) с помощью двоичной математики, где FL - длина дроби.
Отменить любые биты, перенесенные за пределы исходного размера слова.

Например, рассмотрите принятие противоположного значения 11010 (-6). Во-первых, возьмите свой дополнение числа или переверните биты:

$11010 \to 00101$

Затем добавьте 1, обернув все числа в 0 или 1:

$\begin{array}{l} \underline{\begin{array}{r} 00101 \\ + 1 \end{array}} \\ \begin{matrix} 00110 & (6) \end{matrix} \end{array}$

Броски

The fimath объект позволяет вам задать тип данных и масштабирование промежуточных сумм и продуктов с SumMode и ProductMode свойства. Важно иметь в виду последствия каждого приведения, когда вы устанавливаете SumMode и ProductMode свойства. В зависимости от выбранных типов данных может возникнуть переполнение и/или округление. В следующих двух примерах показаны случаи, когда могут происходить переполнение и округление.

Примечание

Дополнительные примеры литья см. в разделе Объекты Cast fi.

Переход от более короткого типа данных к более длинному типу данных

Рассмотрим приведение ненулевого числа, представленного 4-битным типом данных с двумя дробными битами, к 8-битному типу данных с семью дробными битами:

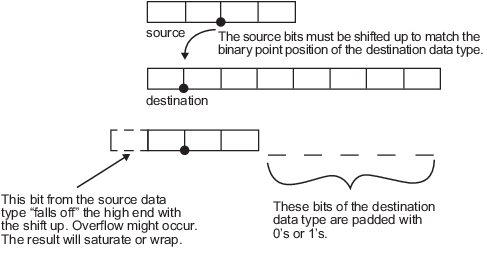
Как показывает схема, исходные биты смещены вверх, так что двоичная точка соответствует двоичному положению точки назначения. Самый высокий бит источника не подходит, поэтому может произойти переполнение, и результат может насытиться или обернуться. Пустые биты в нижнем конце целевого типа данных заполнены либо 0, либо 1-ми:

Если переполнение не происходит, пустые биты заполняются значением 0.
Если происходит перенос, пустые биты заполняются 0.
Если происходит насыщение,
- Пустые биты положительного числа заполнены 1.
- Пустые биты отрицательного числа заполнены 0.

Можно видеть, что даже при приведении от более короткого типа данных к более длинному типу данных все еще может происходить переполнение. Это может произойти, когда целочисленная длина исходного типа данных (в этом случае два) больше, чем целочисленная длина целого типа данных (в этом случае один). Точно так же округление может быть необходимым даже при приведении от более короткого типа данных к более длинному типу данных, если тип данных назначения и масштабирование имеют меньше дробных бит, чем источник.

Переход от более длинного типа данных к более короткому типу данных

Рассмотрим приведение ненулевого числа, представленного 8-битным типом данных с семью дробными битами, к 4-битному типу данных с двумя дробными битами:

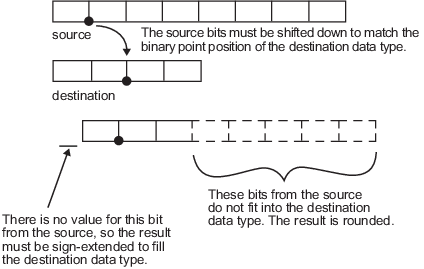
Как показывает схема, исходные биты смещены вниз, так что двоичная точка совпадает с двоичным положением точки назначения. Нет значения для самого высокого бита от источника, поэтому расширение знака используется для заполнения целочисленного фрагмента целевого типа данных. Расширение знака является сложением бит, которые имеют значение самого значительного бита до верхнего конца числа дополнения двух; расширение знака не изменяет значение двоичного числа. Нижние пять биты источника не помещаются в длину части места назначения. Поэтому точность может быть потеряна, когда результат округлен.

В этом случае, даже если приведение от более длинного типа данных до более короткого типа данных, все целочисленные биты поддерживаются. И наоборот, полная точность может быть сохранена, даже если вы приводите к более короткому типу данных, пока длина дроби целевого типа данных является такой же длиной или больше, чем длина дроби исходного типа данных. В этом случае, однако, биты теряются от верхнего конца результата и может произойти переполнение.

Худший случай происходит, когда и целочисленная длина, и длина дроби целевого типа данных короче, чем у исходного типа данных и масштабирования. В этом случае может произойти как переполнение, так и потеря точности.

Документация