Решение использовать оборудование с фиксированной точкой является просто выбором для представления чисел в определенной форме. Это представление часто предлагает преимущества с точки зрения потребления степени, размера, использования памяти, скорости и стоимости конечного продукта.
Измерение физической величины может принимать много числовых форм. Для примера точки кипения воды составляет 100 степени Цельсия, 212 степени Фаренгейта, 373 кельвина или 671,4 степени Ранкина. Независимо от того, какое число задано, физическая величина в точности совпадает. Цифры различаются, потому что используются четыре различных шкалы.
Хорошо известные стандартные шкалы, такие как Цельсий, удобны для обмена информацией. Однако существуют ситуации, когда имеет смысл создавать и использовать уникальные нестандартные шкалы. Эти ситуации обычно включают использование ограниченного ресурса.
Для примера нестандартные шкалы позволяют создателям карт получить максимальную детализацию на листе бумаги фиксированного размера. Типовой дорожный атлас США покажет каждое состояние на двухстраничном отображении. Шкала дюймов к милям будет уникальной для большинства состояний. Используя большое соотношение миль к дюймам, весь Техас может поместиться на двух страницах. Использование той же шкалы для Род-Айленда плохо использовало бы страницу. Использование гораздо меньшего отношения миль к дюймам позволило бы показать Род-Айленд с максимально возможной детализацией.
Аппроксимация измерений переменной внутри встраиваемого процессора подобна подбору кривой карты состояний на листе бумаги. Шкала карты должен позволять помещать все контуры состояния на странице. Точно так же двоичная шкала для измерения должна позволять соответствовать максимальным и минимальным возможным значениям. Шкала карты должна также максимально использовать бумагу в порядок, чтобы получить максимальную детализацию. Точно так же двоичная шкала для измерения должна максимально использовать процессор в порядок, чтобы получить максимальную точность.
Использование стандартных шкал для измерений имеет определенные преимущества совместимости. Однако бывают случаи, когда стоит нарушить соглашение и использовать уникальную нестандартную шкалу. Существуют также случаи, когда сочетание уникальности и совместимости имеет смысл. Для получения дополнительной информации см. следующие разделы.
Предположим, что вы хотите сделать измерения температуры жидкой воды, и что вы хотите представлять эти измерения с помощью 8-битных беззнаковых целых чисел. К счастью, температурная область значений жидкой воды ограничена. Независимо от того, какую шкалу вы используете, жидкая вода может идти только от точки замерзания до точки кипения. Поэтому это область значений температур, которые вы должны захватить, используя только 256 возможные 8-битные значения: 0,1,2,..., 255.
Одним из подходов к представлению температур является использование стандартной шкалы. Для примера модулей для целых чисел может быть Цельсием. Следовательно, целые числа 0 и 100 представляют воду в точке замерзания и в точке кипения, соответственно. С восходящей стороны эта шкала дает тривиальное преобразование из целых чисел в степени Цельсия. На обратной стороне цифры 101-255 не используются. При использовании этой стандартной шкалы было потрачено более 60% области значений числа.
Второй подход - использовать нестандартную шкалу. В этой шкале целые числа 0 и 255 представляют воду в точке замерзания и в точке кипения, соответственно. На восходящей стороне эта шкала дает максимальную точность, так как между замораживанием и кипячением существует 254 значения вместо всего 99. С обратной стороны, модули составляют примерно 0,3921568 степени Цельсия на бит, поэтому преобразование в Цельсия требует деления на 2,55, что является относительно дорогой операцией на большинстве процессоров с фиксированной точкой.
Третий подход заключается в использовании «полустандартной» шкалы. Для примера целые числа 0 и 200 могут представлять воду в точке замерзания и в точке кипения, соответственно. Для этой шкалы модулей 0,5 степеней Цельсия на бит. С обратной стороны, эта шкала не использует цифры от 201-255, что представляет собой потерю более 21%. На повышающей стороне эта шкала позволяет относительно легко преобразовать в стандартную шкалу. Преобразование в Celsius предполагает деление на 2, что является простой операцией сдвига на большинстве процессоров.
Одной из ключевых операций в преобразовании из одной шкалы в другую является умножение. В предыдущем примере приведены три примера преобразования из квантованного целочисленного Q в действительное значение Цельсия V которое включает только умножение:
Графически преобразование представляет собой линию с S уклона, которая должна проходить через источник. Линия через источник называется чисто линейным преобразованием. Ограничение себя чисто линейным преобразованием может быть расточительным, и часто лучше использовать общее уравнение линии:
V = SQ + B.
Добавив термин смещения B, можно получить большую точность при квантовании до ограниченного количества бит.
Общее уравнение линии дает полезное преобразование в квантованную шкалу. Однако, как и все методы квантования, точность ограничена, и преобразование может ввести ошибки. Общее уравнение линии с ошибкой квантования задается как
Если Q квантованного значения округлится до ближайшего представимого числа, то
То есть величина ошибки квантования определяется как количеством бит, так и шкалой. Этот сценарий представляет ошибку наилучшего случая. Для других схем округления ошибка может быть в два раза больше.
На типичных двигателях внутреннего сгорания с электронным управлением поток топлива регулируется таким образом, чтобы получить желаемое отношение воздуха к топливу в цилиндрах непосредственно перед сгоранием. Поэтому требуется знание текущей воздушной скорости потока жидкости. Некоторые производители используют датчики, которые непосредственно измеряют воздушный поток, в то время как другие производители вычисляют воздушный поток из измерений связанных сигналов. Отношение этих переменных определяется из идеального газового уравнения. Идеальное уравнение газа включает деление на температуру воздуха. Для правильных результатов в уравнении должна использоваться абсолютная шкала температуры, такая как кельвин или Ранкин. Однако квантование непосредственно к абсолютной шкале температуры вызовет ненужно большие ошибки квантования.
Температура воздуха, поступающего в двигатель, ограничена областью значений. На типичном двигателе излучатель предназначен для поддержания блока ниже точки кипения охлаждающей жидкости. Предположим, что максимум 225oF (380 К). Когда воздух течет через впускной коллектор, он может нагреваться до этой максимальной температуры. Для холодного старта в экстремальном климате температура может быть до -60oF (222 К). Поэтому, используя абсолютную шкалу кельвина, область значений интереса составляет 222-380 К.
Температура воздуха должна быть квантована для обработки встроенной системой управления. Принимая нереалистичное квантование в 3-битные беззнаковые числа: 0,1,2,..., 7, чисто линейное преобразование с максимальной точностью
Квантованное преобразование и область значений интереса показаны на следующем рисунке.
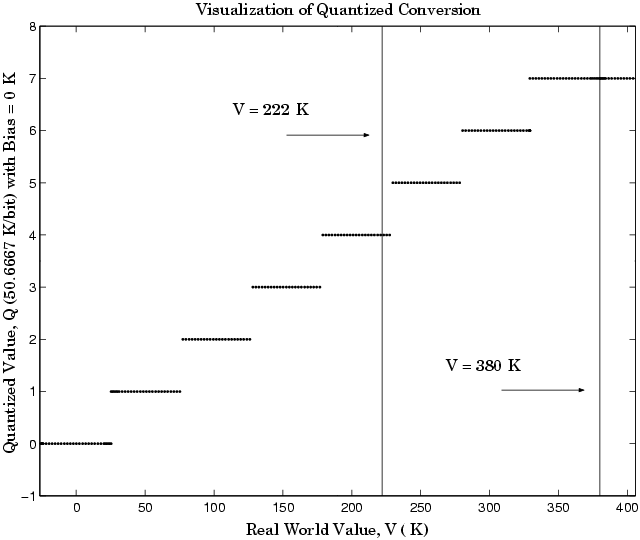
Заметьте, что существует 7,5 возможных значений квантования. Это потому, что только половина первого бита соответствует температурам (реальным значениям), больше нуля.
Ошибка квантования составляет -25,33 К/бит ≤ Error ≤ 25,33 К/бит.
Область значений интереса квантованного преобразования и абсолютное значение квантованной ошибки показаны на следующем рисунке.
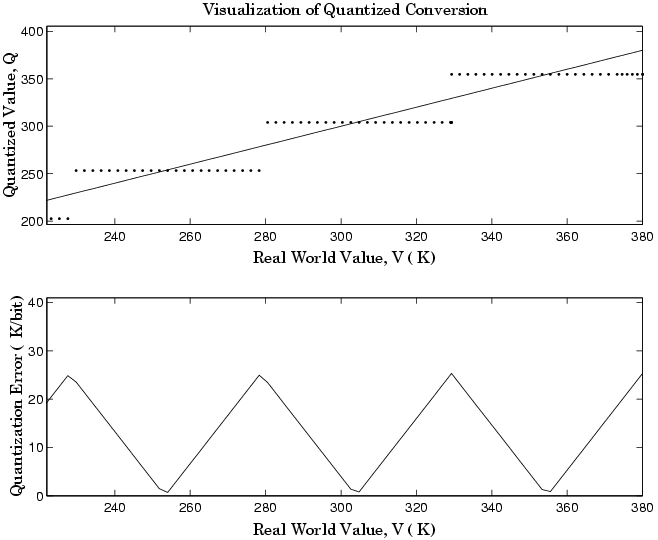
В качестве альтернативы чисто линейному преобразованию рассмотрим общее линейное преобразование с максимальной точностью:
Квантованное преобразование и область значений интереса показаны на следующем рисунке.
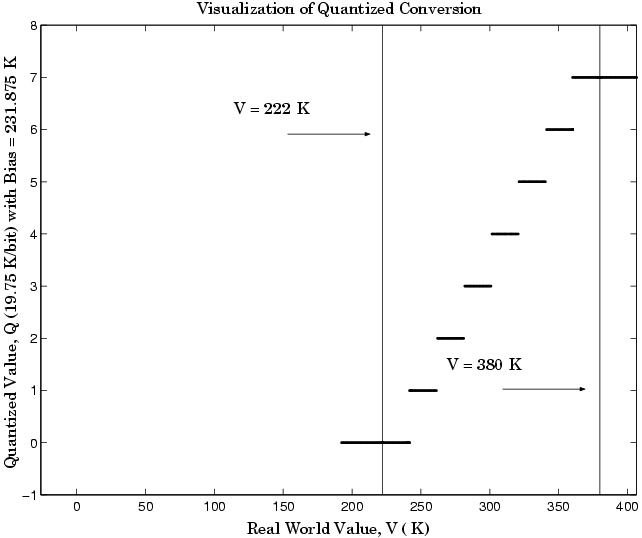
Ошибка квантования составляет -9,875 К/бит ≤ Error ≤ 9,875 К/бит, что примерно в 2,5 раза меньше ошибки, связанной с чисто линейным преобразованием.
Область значений интереса квантованного преобразования и абсолютное значение квантованной ошибки показаны на следующем рисунке.
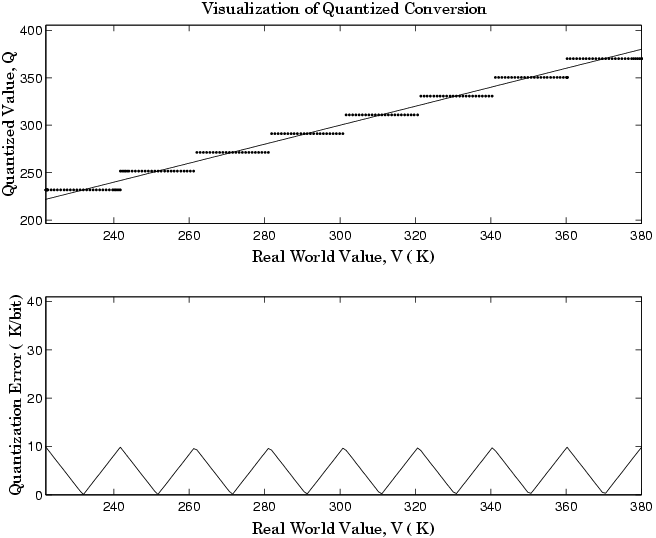
Очевидно, что общая линейная шкала дает гораздо лучшую точность, чем чисто линейная шкала в области значений интересов.