Последовательная каскадная форма
В каскадной форме канонического ряда передаточная функция H (z) записывается как продукт передаточных функций первого и второго порядка:
Это уравнение приводит к каскадной форме канонического ряда.
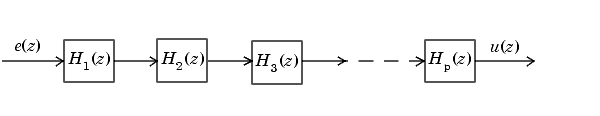
Факторизация H (z) в Hi (z), где i = 1,2,3,..., p может быть выполнена несколькими способами. Используя полюса и нули H (z), можно получить Hi (z) путем группировки пар сопряженных комплексных полюсов и пар сопряженных комплексных нулей для получения передаточных функций второго порядка или путем группировки действительных полюсов и действительных нулей для получения передаточных функций либо первого порядка, либо второго порядка. Можно также сгруппировать два реальных нуля с парой сопряженных комплексных полюсов или наоборот. Поскольку существует много способов получить Hi (z), вы должны сравнить различные группы, чтобы увидеть, что дает лучшие результаты для передаточной функции под фактор.
Для примера одна факторизация H (z) может быть
Необходимо также учитывать, что упорядоченное расположение отдельных Hi (z) приведет к системам с различными числовыми характеристиками. Можно хотеть попробовать различные упорядоченные расположения для заданного набора Hi (z)'s, чтобы определить, какой из них дает лучшие числовые характеристики.
Схема первого порядка для H (z) следующая.
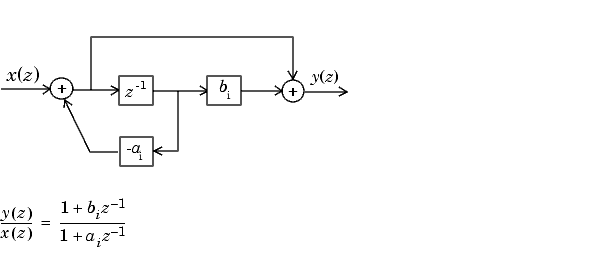
Схема второго порядка для H (z) следующая.
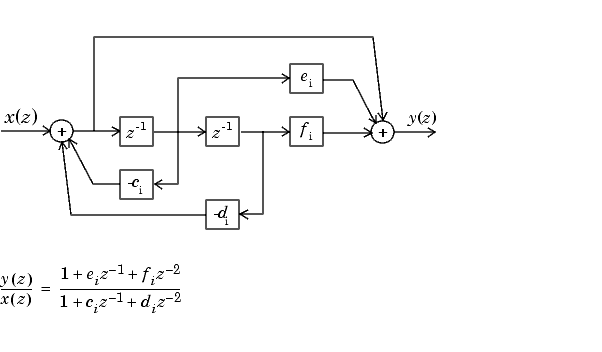
Последовательная каскадная форма примера передаточной функции задается как
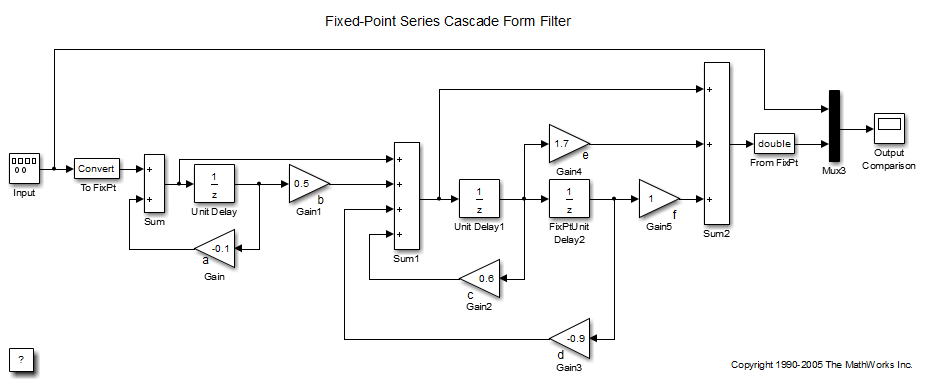
Реализация Hex (z) с использованием Simulink с фиксированной точкой® блоки показаны на следующем рисунке. Вы можете отобразить эту модель путем набора
fxpdemo_series_cascade_form
в MATLAB® командная строка.
