Поиск глобальных или нескольких локальных минимумов

Функция для оптимизации
Единый глобальный минимум через GlobalSearch
Несколько локальных минимумов через MultiStart

Функция для оптимизации

Этот пример иллюстрирует, как GlobalSearch нахождение глобального минимума эффективно и как MultiStart находит еще много локальных минимумов.

Целевая функция для этого примера имеет много локальных минимумов и уникальный глобальный минимум. В полярных координатах функция является

f (r, t) = g (<reservedrangesplaceholder2>) h (<reservedrangesplaceholder0>),

где

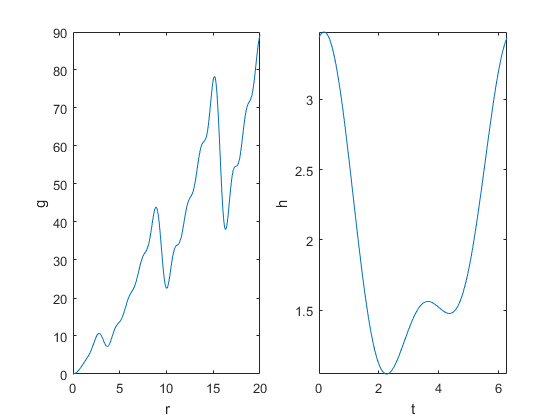
$\begin{matrix} g (r) = (\sin (r) - \frac{\sin (2 r)}{2} + \frac{\sin (3 r)}{3} - \frac{\sin (4 r)}{4} + 4) \frac{r^{2}}{r + 1} \\ h (t) = 2 + \cos (t) + \frac{\cos (2 t - \frac{1}{2})}{2} . \end{matrix}$

Глобальный минимум находится в r = 0, с целевой функцией 0. Функция g (r) растет приблизительно линейно у r с повторяющейся формой пилообразного зуба. Функция h (t) имеет два локальных минимума, один из которых глобальный.

Код для генерации фигуры

Единый глобальный минимум Via GlobalSearch

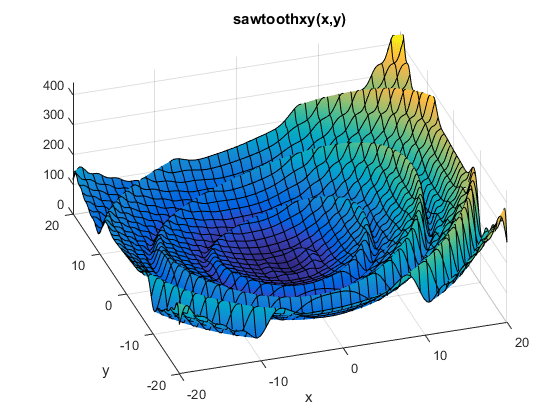
Запишите файл функции, чтобы вычислить цель:

function f = sawtoothxy(x,y)
[t r] = cart2pol(x,y); % change to polar coordinates
h = cos(2*t - 1/2)/2 + cos(t) + 2;
g = (sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) ...
    .*r.^2./(r+1);
f = g.*h;
end

Создайте структуру задачи. Используйте 'sqp' алгоритм для fmincon:
```
problem = createOptimProblem('fmincon',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fmincon,'Algorithm','sqp','Display','off'));
```
Начальная точка [100,-50] вместо [0,0], так GlobalSearch не начинается с глобального решения.
Проверьте структуру задачи путем выполнения fmincon:
```
[x,fval] = fmincon(problem)

x =

   45.7332 -107.6469


fval =

  555.5422
```
Создайте GlobalSearch Объекту и установите итеративное отображение:
```
gs = GlobalSearch('Display','iter');
```

Запустите решатель:

rng(14,'twister') % for reproducibility
[x,fval] = run(gs,problem)

 Num Pts                 Best       Current    Threshold        Local        Local                 
Analyzed  F-count        f(x)       Penalty      Penalty         f(x)     exitflag        Procedure
       0      200       555.5                                   555.5            0    Initial Point
     200     1463   1.547e-15                               1.547e-15            1    Stage 1 Local
     300     1564   1.547e-15     5.858e+04        1.074                              Stage 2 Search
     400     1664   1.547e-15      1.84e+05         4.16                              Stage 2 Search
     500     1764   1.547e-15     2.683e+04        11.84                              Stage 2 Search
     600     1864   1.547e-15     1.122e+04        30.95                              Stage 2 Search
     700     1964   1.547e-15     1.353e+04        65.25                              Stage 2 Search
     800     2064   1.547e-15     6.249e+04        163.8                              Stage 2 Search
     900     2164   1.547e-15     4.119e+04        409.2                              Stage 2 Search
     950     2356   1.547e-15           477        589.7          387            2    Stage 2 Local
     952     2420   1.547e-15         368.4          477        250.7            2    Stage 2 Local
    1000     2468   1.547e-15     4.031e+04        530.9                              Stage 2 Search

GlobalSearch stopped because it analyzed all the trial points.

3 out of 4 local solver runs converged with a positive local solver exit flag.

x =

   1.0e-07 *

    0.0414    0.1298


fval =

   1.5467e-15

Вы можете получить различные результаты, так как GlobalSearch является стохастическим.

Решатель нашел три локальные минимумы, и он нашел глобальный минимум около [0,0].

Несколько локальных минимумов через MultiStart

Запишите файл функции, чтобы вычислить цель:

function f = sawtoothxy(x,y)
[t r] = cart2pol(x,y); % change to polar coordinates
h = cos(2*t - 1/2)/2 + cos(t) + 2;
g = (sin(r) - sin(2*r)/2 + sin(3*r)/3 - sin(4*r)/4 + 4) ...
    .*r.^2./(r+1);
f = g.*h;
end

Создайте структуру задачи. Используйте fminunc решатель со Algorithm значение опции установлено в 'quasi-newton'. Причины такого выбора:
- Проблема без ограничений. Поэтому, fminunc является соответствующим решателем; см. Таблицу принятия решений по оптимизации.
- Дефолт fminunc алгоритм требует градиента; см. Выбор алгоритма. Поэтому задайте Algorithm на 'quasi-newton'.
```
problem = createOptimProblem('fminunc',...
    'objective',@(x)sawtoothxy(x(1),x(2)),...
    'x0',[100,-50],'options',...
    optimoptions(@fminunc,'Algorithm','quasi-newton','Display','off'));
```

Проверьте структуру задачи, запустив ее:

[x,fval] = fminunc(problem)

x =

    1.7533 -111.9488


fval =

  577.6960

Создайте MultiStart по умолчанию объект:
```
ms = MultiStart;
```

Запустите решатель для 50 итераций, записав локальные минимумы:

% rng(1) % uncomment to obtain the same result
[x,fval,eflag,output,manymins] = run(ms,problem,50)

MultiStart completed some of the runs from the start points.

9 out of 50 local solver runs converged with a positive local solver exit flag.

x =

 -142.4608  406.8030


fval =

   1.2516e+03


eflag =

     2


output = 

  struct with fields:

                funcCount: 8586
         localSolverTotal: 50
       localSolverSuccess: 9
    localSolverIncomplete: 41
    localSolverNoSolution: 0
                  message: 'MultiStart completed some of the runs from the start points.↵↵9 out of 50 local solver runs converged with a positive local solver exit flag.'


manymins = 

  1×9 GlobalOptimSolution array with properties:

    X
    Fval
    Exitflag
    Output
    X0

Вы можете получить различные результаты, так как MultiStart является стохастическим.

Решатель не нашел глобальный минимум рядом [0,0]. Он нашел 10 различных местных минимумов.

Постройте график значений функций в локальных минимумах:
```
histogram([manymins.Fval],10)
```
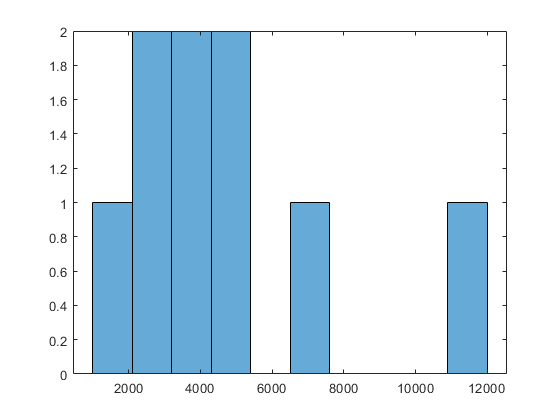
Постройте график значений функций в трех лучших точках:
```
bestf = [manymins.Fval];
histogram(bestf(1:3),10)
```

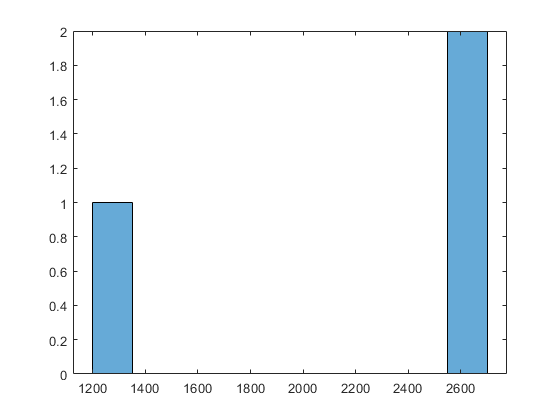
MultiStart начатый fminunc от начальных точек с компонентами, равномерно распределенными между -1000 и 1000. fminunc часто застрял в одном из многочисленных местных минимумов. fminunc превысил предел итерации или предел вычисления функции в 40 раз.

Документация