Документация

Нелинейные ограничения с использованием ga

Предположим, что вы хотите минимизировать простую функцию соответствия двух переменных x 1 и _x 2,

удовлетворяющее следующим нелинейным ограничениям неравенства и границам

Начните с создания функций соответствия и ограничений. Сначала создайте файл с именем simple_fitness.m следующим образом:

function y = simple_fitness(x)
y = 100*(x(1)^2 - x(2))^2 + (1 - x(1))^2;

Функция генетического алгоритма, ga, предполагает, что функция соответствия займет один вход x, где x имеет столько элементов, сколько переменных в задаче. Функция соответствия вычисляет значение функции и возвращает это скалярное значение в своем одном возвращаемом аргументе, y.

Затем создайте файл, simple_constraint.m, содержащего ограничения

function [c, ceq] = simple_constraint(x)
c = [1.5 + x(1)*x(2) + x(1) - x(2);...
-x(1)*x(2) + 10];
ceq = [];

ga функция предполагает, что функция ограничения займет один вход x, где x имеет столько элементов, сколько переменных в задаче. Функция ограничения вычисляет значения всех ограничений неравенства и равенства и возвращает два вектора c и ceq, соответственно.

Чтобы минимизировать функцию соответствия, необходимо передать указатель на функцию соответствия как первый аргумент к ga function, а также указание количества переменных в качестве второго аргумента. Нижняя и верхняя границы предусмотрены следующим LB и UB соответственно. В сложение, вам также нужно передать указатель на функцию в нелинейную функцию ограничения.

ObjectiveFunction = @simple_fitness;
nvars = 2;    % Number of variables
LB = [0 0];   % Lower bound
UB = [1 13];  % Upper bound
ConstraintFunction = @simple_constraint;
rng(1,'twister') % for reproducibility
[x,fval] = ga(ObjectiveFunction,nvars,...
    [],[],[],[],LB,UB,ConstraintFunction)

Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    0.8123   12.3137


fval =

   1.3581e+04

Для задач без целочисленных ограничений решатель генетического алгоритма обрабатывает линейные ограничения и ограничения по-другому по сравнению с нелинейными ограничениями. Все линейные ограничения и ограничения выполняются на протяжении всей оптимизации. Однако, ga может не удовлетворять всем нелинейным ограничениям в каждой генерации. Если ga сходится к решению, нелинейные ограничения будут удовлетворены в этом решении.

Если существуют целочисленные ограничения, ga не применяет допустимость линейных ограничений и вместо этого добавляет любые линейные нарушения ограничений к функции штрафа. См. Целочисленный алгоритм ga.

ga использует функции мутации и кроссовера, чтобы произвести новые индивидуумов в каждой генерации. ga удовлетворяет линейным и связанным ограничениям с помощью мутационных и перекрестных функций, которые только генерируют допустимые точки. Для примера, в предыдущем вызове на ga, функцию мутации mutationguassian не обязательно подчиняется связанным ограничениям. Поэтому, когда существуют связанные или линейные ограничения, значение по умолчанию ga функция мутации mutationadaptfeasible. Если вы предоставляете пользовательскую функцию мутации, эта пользовательская функция должна генерировать только точки, которые допустимы относительно линейных и связанных ограничений. Все включенные функции перекрестия генерируют точки, которые удовлетворяют линейным ограничениям и границам.

Чтобы увидеть прогресс оптимизации, используйте optimoptions функция для создания опций, которые выбирают две функции вывода на функцию построения графика. Первая функция построения графика gaplotbestf, который рисует лучший и средний счет населения на каждой генерации. Вторая функция построения графика gaplotmaxconstr, который строит график максимального нарушения ограничений нелинейных ограничений для каждой генерации. Можно также визуализировать прогресс алгоритма, отобразив информацию в командном окне с помощью 'Display' опция.

options = optimoptions('ga','PlotFcn',{@gaplotbestf,@gaplotmaxconstr},'Display','iter');

Повторно выполните команду ga решатель.

[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],...
              LB,UB,ConstraintFunction,options)

                              Best       Max        Stall
Generation  Func-count        f(x)     Constraint  Generations
    1           2520       13603.6            0      0
    2           4982       13578.2    5.718e-06      0
    3           7538       14033.9            0      0
    4          11116       13573.7    0.0009577      0
Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    0.8122   12.3104


fval =

   1.3574e+04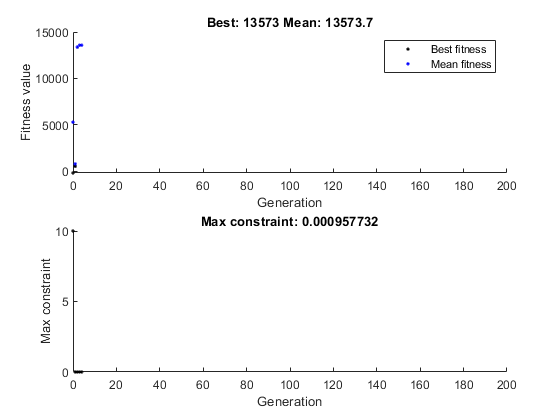

Можно предоставить начальную точку для минимизации ga функция путем определения InitialPopulationMatrix опция. ga функция будет использовать первый индивидуума из InitialPopulationMatrix как начальная точка для ограниченной минимизации.

X0 = [0.5 0.5]; % Start point (row vector)
options = optimoptions('ga',options,'InitialPopulationMatrix',X0);

Теперь перезапустите ga решатель.

[x,fval] = ga(ObjectiveFunction,nvars,[],[],[],[],...
              LB,UB,ConstraintFunction,options)

                              Best       Max        Stall
Generation  Func-count        f(x)     Constraint  Generations
    1           2520       13578.1    0.0005269      0
    2           4982       13578.2    1.815e-05      0
    3           8008       14031.3            0      0
    4          13525       14054.9            0      0
    5          17620       13573.5    0.0009986      0
Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

    0.8122   12.3103


fval =

   1.3573e+04

Похожие темы

• Ограниченная минимизация с использованием генетического алгоритма
• Эффекты опций генетического алгоритма