Генетический алгоритм применяет мутации, используя MutationFcn опция. Опция мутации по умолчанию, @mutationgaussian, добавляет случайное число или мутацию, выбранную из Гауссова распределения, к каждой записи родительского вектора. Обычно количество мутации, которое пропорционально стандартному отклонению распределения, уменьшается у каждой новой генерации. Можно контролировать среднее количество мутации, которую алгоритм применяет к родительскому элементу в каждой генерации через Scale и Shrink входы, которые вы включаете в массив ячеек:
options = optimoptions('ga',... 'MutationFcn',{@mutationgaussian Scale Shrink});
Scale и Shrink являются скалярами со значениями по умолчанию 1 каждый.
Scale управляет стандартным отклонением мутации в первой генерации. Это значение Scale умноженный на область значений начальной генеральной совокупности, который вы задаете на InitialPopulationRange опция.
Shrink контролирует скорость, с которой уменьшается среднее количество мутации. Стандартное отклонение уменьшается линейно, так что его конечное значение равняется 1 - Shrink раз больше его начального значения в первой генерации. Для примера, если у Shrink значение по умолчанию 1затем количество мутации уменьшается до 0 на заключительной стадии.
Эффект мутации можно увидеть, выбрав функции построения графика @gaplotdistance и @gaplotrange, а затем запустил генетический алгоритм над задачей, такой как та, которая описана в Функции Минимизации Растригина. Следующий рисунок показывает график после установки генератора случайных чисел.
rng default % For reproducibility options = optimoptions('ga','PlotFcn',{@gaplotdistance,@gaplotrange},... 'MaxStallGenerations',200); % to get a long run [x,fval] = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options);
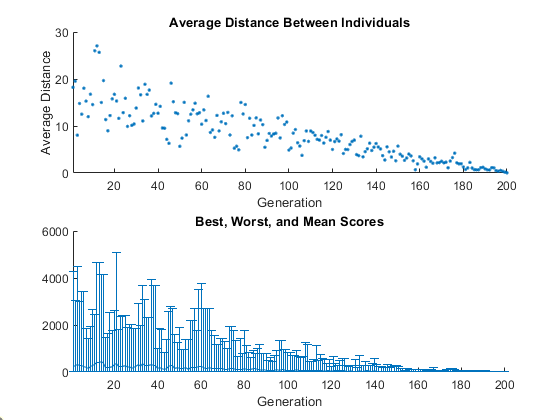
Верхний график отображает среднее расстояние между точками в каждой генерации. Когда количество мутации уменьшается, уменьшается и среднее расстояние между индивидуумами, которое составляет приблизительно 0 в конечной генерации. Нижний график отображает вертикальную линию для каждой генерации, показывая область значений от наименьшего до самого большого значения соответствия, а также среднее значение соответствия. Когда количество мутации уменьшается, уменьшается и область значений. Эти графики показывают, что уменьшение количества мутации уменьшает разнообразие последующих поколений.
Для сравнения, следующий рисунок показывает те же графики, когда вы задаете Shrink на 0.5.
options = optimoptions('ga',options,... 'MutationFcn',{@mutationgaussian,1,.5}); [x,fval] = ga(@rastriginsfcn,2,[],[],[],[],[],[],[],options);

На этот раз среднее количество мутации уменьшается в 1/2 раза к окончательной генерации. В результате среднее расстояние между индивидуумами уменьшается меньше, чем раньше.
The CrossoverFraction опция задает долю каждого населения, кроме элитных дочерних элементов, которые состоят из дочерних элементов кроссовера. Перекрестная доля 1 означает, что все дети, кроме элитных индивидуумов, являются детьми-кроссоверами, в то время как перекрестная часть 0 означает, что все дети являются детьми с мутациями. Следующий пример показывает, что ни одна из этих крайностей не является эффективной стратегией оптимизации функции.
В примере используется функция соответствия, значение которой в точке является суммой абсолютных значений координат в точках. То есть,
Вы можете задать эту функцию как анонимную функцию, задав функцию соответствия равной
@(x) sum(abs(x))
Запустите пример со значением по умолчанию 0.8 как CrossoverFraction опция.
fun = @(x) sum(abs(x)); nvar = 10; options = optimoptions('ga',... 'InitialPopulationRange',[-1;1],... 'PlotFcn',{@gaplotbestf,@gaplotdistance}); rng(14,'twister') % For reproducibility [x,fval] = ga(fun,nvar,[],[],[],[],[],[],[],options)
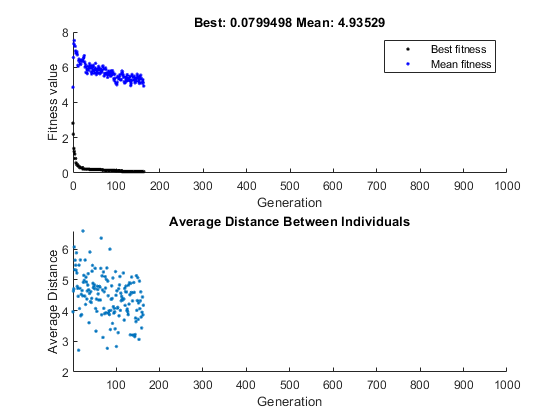
Optimization terminated: average change in the fitness value less than options.FunctionTolerance.
x =
-0.0020 -0.0134 -0.0067 -0.0028 -0.0241 -0.0118 0.0021 0.0113 -0.0021 -0.0036
fval =
0.0799Чтобы увидеть, как работает генетический алгоритм, когда нет мутации, установите CrossoverFraction опция для 1.0 и перезапустите решатель.
options.CrossoverFraction = 1; [x,fval] = ga(fun,nvar,[],[],[],[],[],[],[],options)
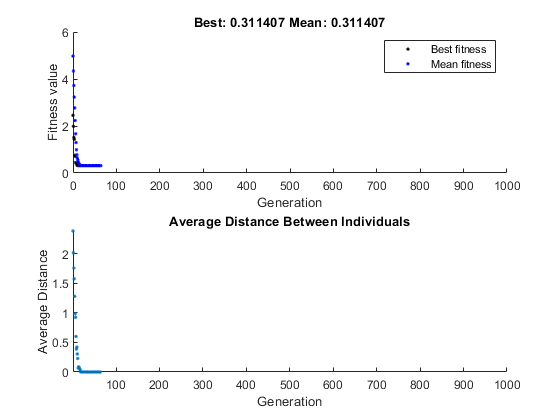
x =
-0.0275 -0.0043 0.0372 -0.0118 -0.0377 -0.0444 -0.0258 -0.0520 0.0174 0.0533
fval =
0.3114Optimization terminated: average change in the fitness value less than options.FunctionTolerance. x = 0.4014 0.0538 0.7824 0.1930 0.0513 -0.4801 0.9988 -0.0059 0.0875 0.0302 fval = 3.0843
При этом алгоритм выбирает гены из индивидуумов в начальную генеральную совокупность и рекомбинирует их. Алгоритм не может создать никаких новых генов, потому что нет мутации. Алгоритм генерирует лучшего индивидуума, которого он может использовать эти гены, в генерации № 8, где лучший график соответствия становится уровнем. После этого он создает новые копии лучшего индивидуума, которые затем отбираются для следующей генерации. По генерации № 17 все индивидуумы в населении одинаковы, а именно - лучший индивидуум. Когда это происходит, среднее расстояние между индивидуумами составляет 0. Поскольку алгоритм не может улучшить лучшее значение соответствия после генерации 8, он останавливается после еще 50 генерации, потому что Stall generations установлено на 50.
Чтобы увидеть, как работает генетический алгоритм, когда нет кроссовера, установите CrossoverFraction опция для 0.
options.CrossoverFraction = 0; [x,fval] = ga(fun,nvar,[],[],[],[],[],[],[],options)

В этом случае случайные изменения, которые применяет алгоритм, никогда не улучшают значение соответствия лучшего индивидуума в первой генерации. Хотя он улучшает отдельные гены других индивидуумов, как вы можете видеть на верхнем графике путем уменьшения среднего значения функции соответствия, эти улучшенные гены никогда не сочетаются с генами лучшего индивидуума, потому что нет никакого кроссовера. В результате, лучший график соответствия является уровнем, и алгоритм застопорится на генерации № 50.
Пример deterministicstudy.m, который входит в программное обеспечение, сравнивает результаты применения генетического алгоритма к функции Растригина с CrossoverFraction значение опции установлено в 0, .2, .4, .6, .8, и 1. Пример работает в течение 10 генерации. В каждой генерации пример строит графики средств и стандартных отклонений лучших значений соответствия во всех предыдущих поколениях для каждого значения CrossoverFraction опция.
Чтобы запустить пример, введите
deterministicstudy
в MATLAB® приглашение. Когда пример закончен, графики появляются как на следующем рисунке.
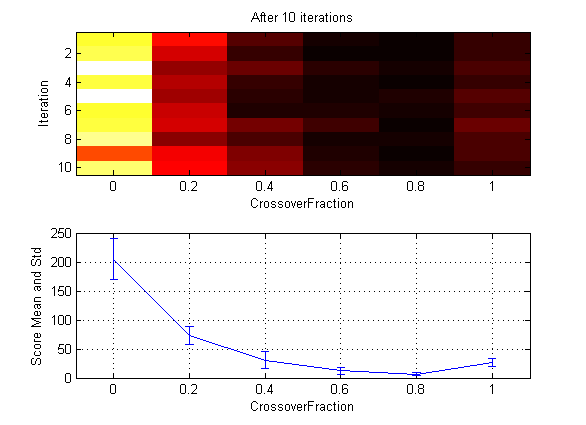
Нижний график показывает средние и стандартные отклонения лучших значений соответствия за 10 генерацию для каждого из значений перекрестной фракции. Верхний график показывает цветное отображение лучших значений соответствия в каждой генерации.
Для этой функции соответствия, устанавливая Crossover fraction на 0.8 приводит к лучшему результату. Однако для другой функции соответствия, другая настройка для Crossover fraction может дать лучший результат.