Можно построить симулированный отклик модели, используя импульсные и шаговые сигналы в качестве входов для всех линейных параметрических моделей и корреляционных (непараметрических) моделей.
Можно также создать переходные процессы для нелинейных моделей. Эти графики шага и импульсной характеристики, также называемые временными графиками переходного процесса, обеспечивают понимание характеристик динамики модели, включая максимальную чувствительность и время урегулирования.
Примечание
Для моделей частотной характеристики импульсы и переходные процессы недоступны. Для нелинейных моделей доступны только переходные процессы.
Переходные процессы обеспечивают понимание основных динамических свойств модели, таких как время отклика, статическое усиление и задержки.
Переходные процессы также помогают вам проверить, насколько хорошо линейная параметрическая модель, такая как линейная модель ARX или модель пространства состояний, захватывает динамику. Например, можно оценить импульс или переходную характеристику от данных с помощью корреляционного анализа (непараметрическая модель), а затем построить график результата корреляционного анализа поверх переходных процессов параметрических моделей.
Поскольку непараметрические и параметрические модели получают с помощью различных алгоритмов, согласие между этими моделями увеличивает доверие в результатах параметрической модели.
Переходные процессы показывают значение импульса или переходной характеристики на вертикальной оси. Горизонтальная ось находится в модулях времени, заданных для данных, используемых для оценки модели.
Импульсная характеристика динамической модели является выходом сигналом, который результаты, когда вход является импульсом. То есть u (t) является нулем для всех значений t, кроме t = 0, где u (0) = 1. В следующем разностном уравнении можно вычислить импульсную характеристику путем установки y (-T) = y (-2T) = 0, u (0) = 1 и u (t > 0) = 0.
Ответ шага является выходным сигналом, который возникает из шага входа, где u (t < 0) = 0 и u (t > 0) = 1.
Если ваша модель включает шумовую модель, можно отобразить переходный процесс шумовой модели, связанной с каждым выходам каналом. Для получения дополнительной информации о том, как отобразить переходный процесс модели шума, смотрите Plot Impulse и Переходная Характеристика Using the Система Идентификации App.
Следующий рисунок показывает пример Переходному процессу графика, созданный в приложении Системы идентификации.
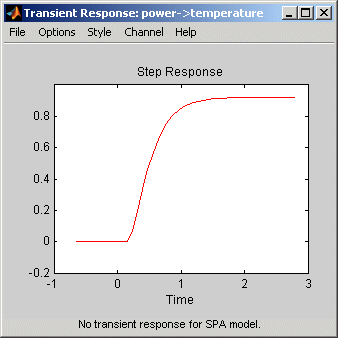
В сложение к кривой переходного процесса можно отобразить на графике доверия интервал. Чтобы узнать, как показать или скрыть доверие интервал, смотрите описание настроек графика в Plot Impulse и Переходную характеристику Using the Системы идентификации App.
Доверительный интервал соответствует области значений отклика с определенной вероятностью того, что это фактическая реакция системы. Тулбокс использует предполагаемую неопределенность в параметрах модели, чтобы вычислить доверительные интервалы и принимает, что оценки имеют Гауссово распределение.
Для примера для интервала 95% доверия область вокруг номинальной кривой представляет области значений, где существует 95% вероятность того, что она содержит истинный отклик системы. Можно задать доверительный интервал как вероятность (между 0 и 1) или как количество стандартных отклонений Гауссова распределения. Для примера вероятность 0,99 (99%) соответствует 2,58 стандартных отклонений.
Примечание
Вычисление интервала доверия принимает, что модель достаточно описывает динамику системы и модель, невязки пройти тесты независимости.