Можно создать диаграммы нулей и полюсов линейных идентифицированных моделей. Чтобы изучить полюса и нули шумового компонента модели ввода-вывода или модели временных рядов, используйте noise2meas для первого извлечения модели шума как независимой модели ввода-вывода, входами которой являются шумовые каналы исходной модели.
Для примеров создания графиков с нулем полюсов смотрите Model Poles and Neros Using the Система Идентификации App и Plot Poles and Zeros в командной строке.
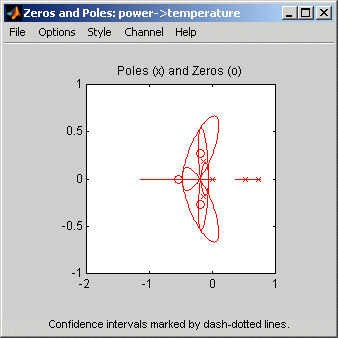
Следующий рисунок показывает выборку диаграммы нулей и полюсов модели с доверием интервалами. x указание полюсов и o указать нули.
Общее уравнение линейной динамической системы задается:
В этом уравнении G является оператором, который принимает вход в выход и захватывает динамику системы, и v является термином аддитивного шума.
Полюса линейной системы являются корнями знаменателя передаточной функции G. Полюса оказывают непосредственное влияние на динамические свойства системы. Нули являются корнями числителя G. Если вы оценили модель шума H в дополнение к динамической модели G, можно также просмотреть полюса и нули модели шума.
Нули и полюсы являются эквивалентными способами описания коэффициентов линейного разностного уравнения, такого как модель ARX. Поляки связаны с выходом стороной разностного уравнения, а нули связаны с входом стороной уравнения. Количество полюсов равно количеству интервалов дискретизации между наиболее задержанным и наименее задержанным выходом. Количество нулей равно количеству интервалов дискретизации между наиболее задержанным и наименее задержанным входом. Для примера существует два полюса и один нуль в следующей модели ARX:
Можно отобразить интервал доверия для каждого шеста и нуля на графике. Чтобы узнать, как показать или скрыть доверительный интервал, смотрите Model Poles and Neros Using the Система Идентификации App и Plot Poles and Neros в командной строке.
Доверительный интервал соответствует области значений полюса или нуля с определенной вероятностью быть фактическим полюсом или нулями системы. Тулбокс использует предполагаемую неопределенность в параметрах модели, чтобы вычислить доверительные интервалы и принимает, что оценки имеют Гауссово распределение.
Для примера для интервала доверия 95% область вокруг номинального полюса или нуля значения представляет области значений значений, которые имеют 95% вероятность быть истинным системным полюсом или нулем значением. Можно задать доверительный интервал как вероятность (между 0 и 1) или как количество стандартных отклонений Гауссова распределения. Для примера вероятность 0,99 (99%) соответствует 2,58 стандартных отклонений.
Можно использовать диаграммы нулей и полюсов, чтобы оценить, может ли быть полезно уменьшить порядок модели. Когда доверие интервалы для перекрытия пара полюс-ноль, это перекрытие указывает на возможное удаление нулей-полюсов. Для получения дополнительной информации см. «Уменьшение порядка модели с использованием Диаграмм нулей и полюсов».