Вы можете получить доступ к местоположениям на изображениях, используя несколько различных систем координат изображений. Можно задать местоположения с помощью дискретных индексов пикселей, поскольку изображения хранятся в виде массивов. Можно также задать местоположения с помощью непрерывных пространственных координат, потому что изображения представляют реальные сцены в непрерывном пространстве.
Как описано в Изображениях в MATLAB, MATLAB® сохраняет большинство изображений как массивы. Каждый (строка, столбец) индекс массива соответствует одному пикселю в отображаемом изображении.
Существует соответствие один к одному между индексами пикселей и нижними индексами для первых двух матричных размерностей. Так же, как и для индексации массива в MATLAB, индексы пикселей являются целочисленными значениями и варьируются от 1 до длины строки или столбца. Индексы упорядочиваются сверху вниз и слева направо.
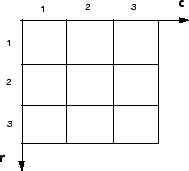
Для примера данные для пикселя в пятой строке, втором столбце сохраняются в элемент матрицы (5,2). Вы используете нормальные матрицы индексирования MATLAB для доступа к значениям отдельных пикселей. Для примера, код MATLAB
I(2,15)
возвращает значение пикселя в строке 2, столбец 15 одноканального изображения I. Аналогично, код MATLAB
RGB(2,15,:)
возвращает значения цвета пикселя в строке 2, столбец 15 многоканального изображения RGB.
В пространственной системе координат положения на изображении являются положениями на непрерывной плоскости. Местоположения описаны в терминах Декартовых x и y координат (а не индексов строк и столбцов, как в системе индексации пикселей). С этой Декартовой точки зрения (x, y) местоположение, такое как (3,2,5,3), является значимым и отличным от координаты (5,3).
Image Processing Toolbox™ задает два типа пространственных систем координат в зависимости от системы ссылки. Внутренние координаты задают местоположения относительно системы координат ссылки изображения. Мировые координаты определяют местоположения относительно внешнего наблюдателя мира.
По умолчанию тулбокс задает пространственные координаты изображения с помощью внутренней системы координат. Эта пространственная система координат соответствует индексам пикселей изображения. Внутренние координаты (x, y) центральной точки любого пикселя идентичны индексам столбца и строки для этого пикселя. Для примера центральная точка пикселя в строке 5, столбец 3 имеет пространственные координаты x = 3.0, y = 5.0. Однако следует иметь в виду, что порядок внутренней координаты (3,0,5,0) изменяется назад относительно индексов пикселей (5,3).
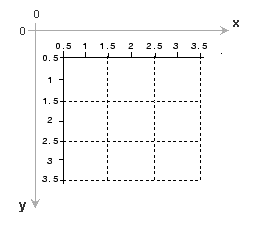
Внутренние координаты центра каждого пикселя являются целочисленными. Центр верхнего левого пикселя имеет внутренние координаты (1.0, 1.0). Центр нижнего правого пикселя имеет внутренние координаты (numCols, numRows), где numCols и numRows количество строк и столбцов в изображении. В целом центр пикселя с пиксельными индексами (m, n) падает в точке x = n, y = m в внутренней системе координат.
Поскольку размер каждого пикселя в внутренней системе координат равен одному модулю, контуры изображения имеют дробные координаты. Верхний левый угол изображения расположен на (0.5,0,5), а не на (0,0). Точно так же нижний правый угол изображения расположен в (numCols + 0.5, numRows + 0.5).
Несколько функций в основном работают с пространственными координатами, а не с индексами пикселей, но пока вы используете систему пространственных координат по умолчанию (внутренние координаты), можно задать местоположения с точки зрения их столбцов (x) и строк (y).
В некоторых ситуациях может потребоваться использовать мировую систему координат (также называемую недефолтной пространственной системой координат). Некоторые ситуации, когда может потребоваться использовать мировую систему координат, включают:
Когда вы выполняете геометрическую операцию, такую как перемещение, над изображением и хотите сохранить информацию о том, как новая позиция относится к исходному положению.
Когда пиксели не квадратные. Для примера в магнитно-резонансной томографии (МРТ) данные можно собрать таким образом, чтобы пиксели имели более высокую частоту дискретизации в одном направлении, чем ортогональное направление.
Когда вы знаете, как степень пикселей выравнивается с положениями в реальном мире. Для примера на аэрофотоснимке каждый пиксель может охватывать конкретную закрашенную фигуру на 5 метров на земле.
Когда необходимо изменить направление оси x -ось или y -ось. Это распространенный метод для использования с геопространственными данными.
Существует несколько способов задать мировую систему координат. Можно использовать пространственные объекты привязки, которые кодируют местоположение изображения в мировой системе координат, разрешение изображения и отношение объема изображения к внутренним и мировым координатам. Можно также задать максимальную и минимальную координаты в каждой размерности. Для получения дополнительной информации смотрите Задать мировую систему координат изображения.