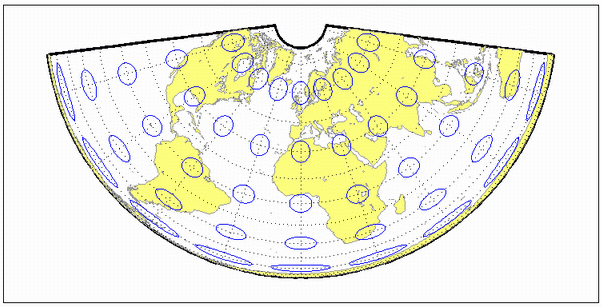
Коническая проекция Альберса с равной площадью
Конический
eqaconic
Меридианы: Равномерно расположенные прямые линии, сходящиеся к общей точке, обычно за полюсом. Углы между меридианами меньше истинных углов.
Параллели: Неравномерно расположенные концентрические дуги с центром от точки сходимости. Интервал между параллелями уменьшается от центральных широт.
Поляки: Обычно круглые дуги, заключающие в себе тот же угол, что и отображаемые параллели.
Симметрия: О любом меридиане.
Это проекция равной площади. Шкала верна вдоль одной или двух выбранных стандартных параллелей. Шкала постоянна вдоль любой параллели; масштабный коэффициент меридиана в любой заданной точке является обратным коэффициенту вдоль параллели для сохранения равной площади. Этот выступ свободен от искажений вдоль стандартных параллелей. Искажение постоянно вдоль любой другой параллели. Этот выступ не является ни конформным, ни равноудаленным.
Конус проекции имеет интересные ограничительные формы. Если шест выбран в качестве одной стандартной параллели, конус является плоскостью, и результаты проекции Lambert Azimuthal Equal-Area. Если выбраны две параллели, не симметричные относительно Экватора, то получается коническая проекция Ламберта с равной площадью. Если в качестве одной из стандартных параллелей выбран полюс, то проективный полюс является точкой, в противном случае проективный полюс является дугой. Если Экватор выбран как одна параллель, конус становится цилиндром, и результатом является проекция Ламберта с равной площадью. Наконец, если в качестве стандартных параллелей выбраны две параллели, равноудаленные от Экватора, то результатом является Бехрманн или другая цилиндрическая проекция равной площади. Предлагаемые параллели для карт контерминозных США [29,5 45,5]. Параллели по умолчанию [15 75].
Данные о долготе, превышающей 135º к востоку или западу от центрального меридиана, обрезаны.
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('eqaconic', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;