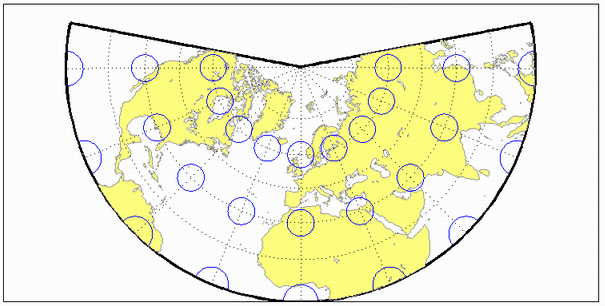
Конформная коническая проекция Ламберта
Конический
lambert
Меридианы: Равноотстоящие прямые линии, сходящиеся на одном из полюсов. Углы между меридианами меньше истинных углов.
Параллели: Неравномерно расположенные концентрические круговые дуги с центром на полюсе сходимости. Интервал между параллелями увеличивается от центральных широт.
Поляки: Полюс, ближайший к стандартной параллели, является точкой, другой не может быть показан.
Симметрия: О любом меридиане.
Шкала верна вдоль одной или двух выбранных стандартных параллелей. Шкала является постоянной вдоль любой параллели и одинаковой в каждом направлении в любой точке. Этот выступ свободен от искажений вдоль стандартных параллелей. Искажение постоянно вдоль любой другой параллели. Эта проекция конформна везде, кроме полюсов; она не является ни равной по площади, ни равноудаленной.
Конус проекции имеет интересные ограничительные формы. Если полюс выбран в качестве одной стандартной параллели, конус является плоскостью, и получается Стереографическая Азимутальная проекция. Если выбраны две параллели, не симметричные относительно Экватора, то получается проекция Ламберта Конформного Коника. Если в качестве одной из стандартных параллелей выбран полюс, то проективный полюс является точкой, в противном случае проективный полюс является дугой. Если в качестве стандартных параллелей выбраны Экватор или две параллели, равноудаленные от Экватора, конус становится цилиндром, и результат проекции Меркатора. Параллели по умолчанию [15 75].
Эта проекция была представлена Иоганном Генрихом Ламбертом в 1772 году и также известна как коническая ортоморфная проекция.
Данные о долготе, превышающей 135º к востоку или западу от центрального меридиана, обрезаны. Пределы карты по умолчанию являются [0 90], чтобы избежать экстремального искажения области.
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('lambert', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;