Несмотря на то, что Земля очень круглая, это скользящая spheroid, а не совершенная сфера. Это различие настолько мало (только одна часть в 300), что для создания мелкомасштабных (мировых или континентальных) карт достаточно моделирования Земли как сферической. Однако для создания точных карт в больших шкалах требуется использовать сферическую модель. Такие модели необходимы, например, когда вы отображаете спутниковые или воздушные снимки высокого разрешения или когда вы работаете с координатами из Глобальной системы позиционирования (GPS). В этом разделе рассматривается, как программное обеспечение Mapping Toolbox™ точно моделирует форму или рисунок Земли.
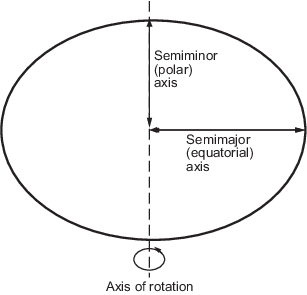
Можно задать эллипсоиды несколькими способами. Они обычно заданы semimajor и semiminor axis, но часто выражаются в терминах большой оси и либо inverse flattening (которая для Земли, как упомянуто выше, является одной частью в 300), либо eccentricity. Какие бы параметры ни использовались, пока включена длина оси, эллипсоид полностью ограничен, а другие параметры производны. Компоненты эллипсоида показаны на следующей схеме.
Тулбокс включает эллипсоидные модели, которые представляют рисунки Солнца, Луны и планет, а также набор наиболее распространенных эллипсоидных моделей Земли. Для получения дополнительной информации смотрите Опорные сфероиды.
Буквально под геоидом подразумевается земная форма. Геоид является эмпирическим приближением рисунка Земли (минус топографический рельеф), её «комом». В частности, это эквипотенциальная поверхность относительно силы тяжести, более или менее соответствующая среднему уровню моря. Это примерно эллипсоид, но не совсем так, потому что локальные изменения силы тяжести создают незначительные холмы и дейлы (которые варьируются от -100 м до + 60 м по всей Земле). Это изменение высоты составляет порядка 1 процента различий между большой и малой эллипсоидными осями, используемыми для аппроксимации формы Земли.
Форма геоида важна для некоторых целей, таких как вычисление орбит спутника, но не должна учитываться для каждого приложения отображения. Однако знание геоида иногда необходимо, например, когда вы сравниваете повышения, заданные как высота над средним уровнем моря, с повышениями, полученными из измерений GPS. Представления геоидов также присущи определениям данных величин.
Получите геоидные высоты и географические проводки ссылки объекта из EGM96 геоидной модели. Загрузка данных о широте и долготе береговой линии.
[N,R] = egm96geoid;
load coastlinesОтобразите высоты геоидов как поверхность с помощью проекции Робинсона. Убедитесь, что данные о береговой линии появляются над поверхностью путем установки 'CData' Пара "имя-значение" к данным о высоте геоидов и 'ZData' пара "имя-значение" в матрицу нулей. Затем отобразите данные береговой линии.
axesm robinson Z = zeros(R.RasterSize); geoshow(N,R,'DisplayType','surface','CData',N,'ZData',Z) geoshow(coastlat,coastlon,'color','k')
Отобразите шкалу палитры под картой.
colorbar('southoutside')