Этот пример показывает, как решить уравнение тепла, которое описывает диффузию тепла в теле. Этот пример использует приложение PDE Modeler. Для программного процесса смотрите Теплопередачу в блоке с полостью.
Рассмотрим блок, содержащий прямоугольную трещину или полость. Левая сторона блока нагревается до 100 степеней С. В правой части блока тепло течет от блока к окружающему воздуху с постоянной скоростью, например -10 Вт/м2. Все остальные контуры изолированы. Температура в блоке в начальное время t 0 = 0 составляет 0 градусов. Цель состоит в том, чтобы смоделировать распределение тепла в течение первых пяти секунд.
УЧП, управляющая этой задачей, является параболическим тепловым уравнением. Partial Differential Equation Toolbox™ решает типовой параболический УЧП вида
Тепловое уравнение имеет вид:
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие шаги:
Откройте приложение PDE Modeler при помощи pdeModeler команда.
pdeModeler
Моделируйте геометрию: рисуйте прямоугольник с углами (-0,5, -0,8), (0,5, -0,8), (0.5,0,8), и (-0,5,0,8) и прямоугольник с углами (-0,05, -0,4), (0.05, -0,4), (0.05,0,4), и (-0,05,0 Нарисуйте первый прямоугольник при помощи pderect функция.
pderect([-0.5 0.5 -0.8 0.8])
Отображение линий сетки с дополнительными тактами в -0.05 и 0.05. Для этого выберите Options > Grid Spacing, снимите флажок Auto и введите X-axis extra ticks по адресу -0.05 и 0.05. Затем выберите Options > Grid.
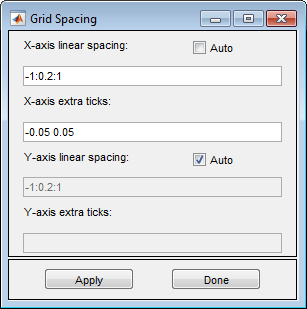
Установите x предел оси равным [-0.6 0.6] и y предел оси [-1 1]. Для этого выберите Options > Axes Limits и установите соответствующие области значений.
Выберите Options > Snap, чтобы выровнять любую новую форму по линиям сетки. Затем нарисуйте прямоугольник с углами (-0,05, -0,4), (0.05, -0,4), (0.05,0,4) и (-0.05,0,4)
Моделируйте геометрию путем ввода R1-R2 в поле Set formula.
Проверьте, что в прикладном режиме задано Generic Scalar.
Задайте граничные условия. Для этого перейдите в граничный режим путем выбора Boundary > Boundary Mode. Затем выберите Boundary > Specify Boundary Conditions и задайте граничное условие Неймана.
Для удобства сначала задайте изолирующее условие контура Неймана ∂ u/ ∂ n = 0 для всех контуров. Для этого выделите все контуры при помощи Edit > Select All и задайте g = 0, q = 0.
Задайте граничное условие Дирихле u = 100 для левой стороны блока. Для этого задайте h = 1, r = 100.
Задайте условие контура Неймана ∂ u/ ∂ n = -10 для правой стороны блока. Для этого задайте g = -10, q = 0.
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Тепловое уравнение является параболическим уравнением, поэтому выберите Parabolic тип PDE. Задайте c = 1, a = 0, f = 0, и d = 1.
Инициализируйте mesh путем выбора Mesh > Initialize Mesh. Уточнить mesh можно путем выбора Mesh > Refine Mesh.
Установите начальное значение 0, время решения 5 секунд и вычислите решение каждые 0,5 секунды. Для этого выберите Solve > Parameters. В диалоговом окне Solve Parameters установите время на 0:0.5:5, и u (t 0), чтобы 0.
Решить УЧП можно путем выбора Solve > Solve PDE или нажатия кнопки = на панели инструментов. Приложение решает уравнение тепла в 11 различных временах от 0 до 5 секунд и отображает распределение тепла в конце временного интервала.
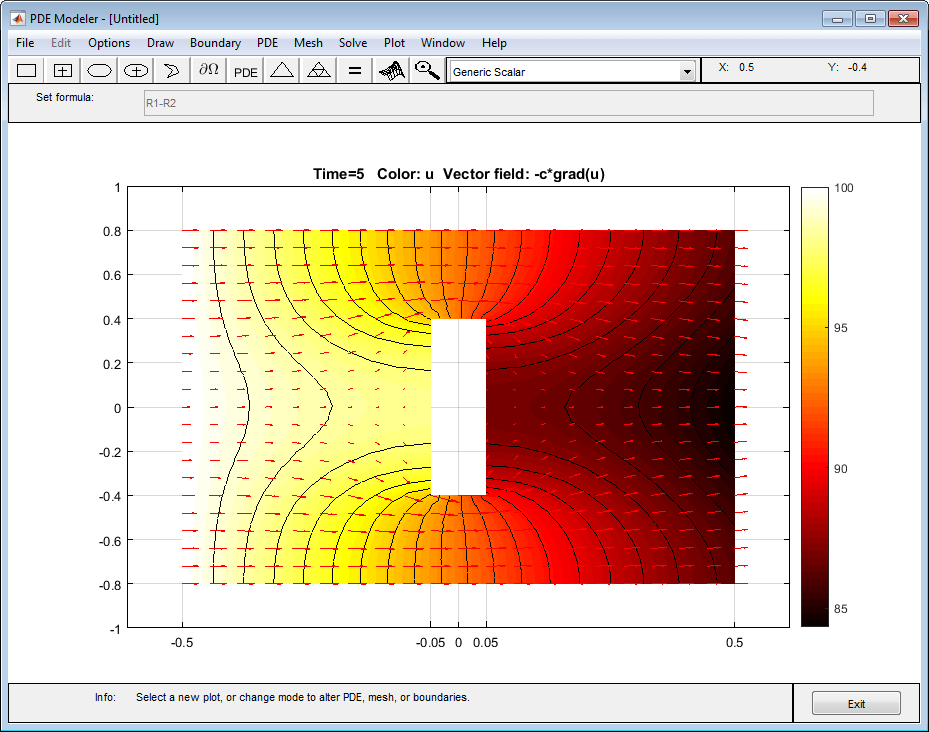
Постройте графики изотермических линий с помощью контурного графика и векторного поля теплового потока с помощью стрел и измените палитру на hot. Для этого:
Выберите Plot > Parameters.
В получившемся диалоговом окне выберите Color, Contour и опции Arrows. Выберите -c*grad(u) из Arrows меню.
Измените палитру на hot при помощи соответствующего раскрывающегося меню в том же диалоговом окне.
Используйте анимированный график, чтобы визуализировать динамическое поведение температуры. Для этого выберите Plot > Parameters и затем выберите опцию Animation.
Температура в блоке повышается очень быстро. Чтобы улучшить анимацию и сосредоточиться на первой секунде, измените список раз на MATLAB® выражение logspace(-2,0.5,20). Для этого выберите Solve > Parameters. В диалоговом окне Solve Parameters установите время на logspace(-2,0.5,20).
Можно исследовать решение, варьируя параметры модели и строя график результатов. Для примера измените коэффициент теплоемкости d и тепловой поток на правом контуре, чтобы увидеть, как эти параметры влияют на распределение тепла.