Решите следующую проблему теплопередачи с различными параметрами материала. Этот пример использует приложение PDE Modeler. Для решений командной строки смотрите Теплопередачу между двумя квадратами из разных материалов.
Геометрия 2-D для этой задачи является квадратом с вложенным алмазом (квадрат с поворотом на 45 степени). УЧП, управляющая этой задачей, является параболическим тепловым уравнением:
где ρ - плотность, C - теплоемкость, k - коэффициент теплопроводности, Q - источник тепла, h - коэффициент конвективной теплопередачи, и T ext - внешняя температура.
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие шаги:
Моделируйте геометрию: рисуйте квадратную область с углами в (0,0), (3,0), (3,3) и (0,3) и алмазообразную область с углами в (1.5,0,5), (2.5,1,5), (1.5,2,5) и (0.5,1,5).
pderect([0 3 0 3]) pdepoly([1.5 2.5 1.5 0.5],[0.5 1.5 2.5 1.5])
Установите x предел оси равным [-1.5 4.5] и y предел оси [-0.5 3.5]. Для этого выберите Options > Axes Limits и установите соответствующие области значений.
Установите режим приложения равным Heat Transfer.
Температура на всех внешних контурах поддерживается равной 0, поэтому вы не должны изменять граничное условие Дирихле по умолчанию T = 0.
Задайте коэффициенты. Для этого выберите PDE > PDE Mode. Затем щелкните каждую область и выберите PDE > PDE Specification или нажмите кнопку PDE на панели инструментов. Поскольку вы решаете параболическое тепловое уравнение, выберите Parabolic тип PDE для обеих областей. Для квадратной области задайте следующие коэффициенты:
Плотность, pho = 2
Теплоемкость, C = 0.1
Коэффициент теплопроводности, k = 10
Источник тепла, Q = 0
Коэффициент конвективной теплопередачи, h = 0
Внешняя температура, Text = 0
Для алмазообразной области задайте следующие коэффициенты:
Плотность, pho = 1
Теплоемкость, C = 0.1
Коэффициент теплопроводности, k = 2
Источник тепла, Q = 4
Коэффициент конвективной теплопередачи, h = 0
Внешняя температура, Text = 0
Инициализируйте mesh путем выбора Mesh > Initialize Mesh. Для получения более точного решения уточните mesh путем выбора Mesh > Refine Mesh.
Установите начальное значение и время решения. Для этого выберите Solve > Parameters.
Динамика для этой задачи очень быстрая - температура достигает устойчивого состояния примерно в 0,1 временные модули. Чтобы захватить интересную часть динамики, установите время на logspace(-2,-1,10). Это дает 10 логарифмически разнесенных чисел между 0,01 и 0,1. Установите начальное значение u температуры (t 0) равным 0.
Решить уравнение можно, выбрав Solve > Solve PDE или нажав кнопку = на панели инструментов.
Постройте график решения. По умолчанию приложение строит график распределения температуры в последний раз. Лучший способ визуализировать динамическое поведение температуры - это анимировать решение. Для этого выберите Plot > Parameters и выберите опции Animation и Height (3-D plot), чтобы анимировать 3-D график. Кроме того, можно выбрать опцию Plot in x-y grid для использования прямоугольной сетки вместо используемой по умолчанию треугольной сетки. Использование прямоугольной сетки вместо треугольной значительно ускоряет процесс анимации.
Можно также построить график изотермических линий с помощью контурного графика и векторного поля теплового потока со стрелами.
Выберите Plot > Parameters.
В получившемся диалоговом окне отмените выбор Animation, и Height (3-D plot), и Plot in x-y grid опций.
Измените палитру на hot при помощи соответствующего раскрывающегося меню в том же диалоговом окне.
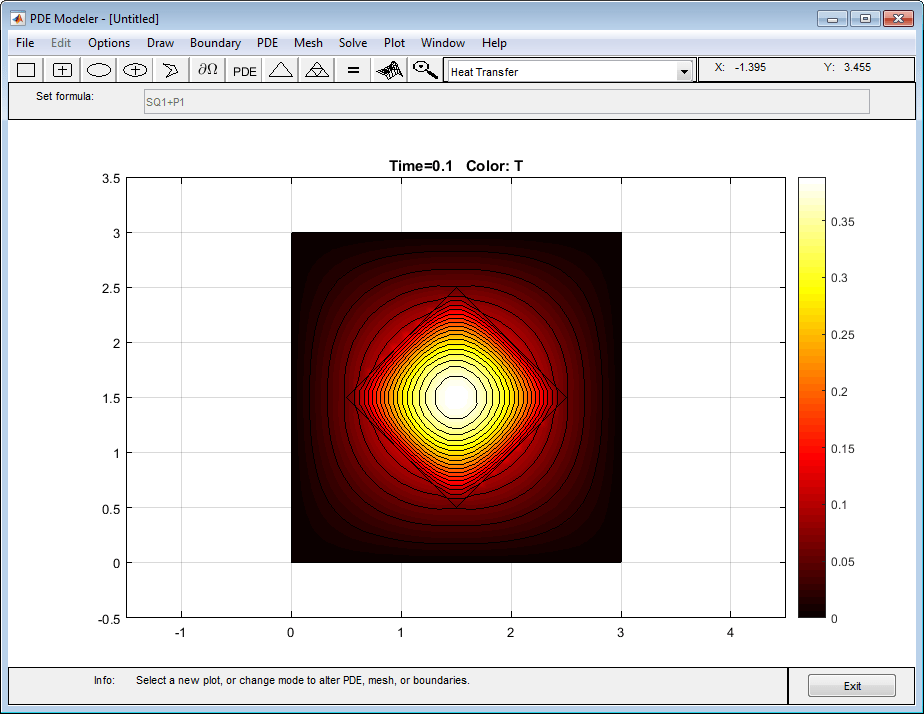
Чтобы получить первый график, выберите Color и Contour опции.
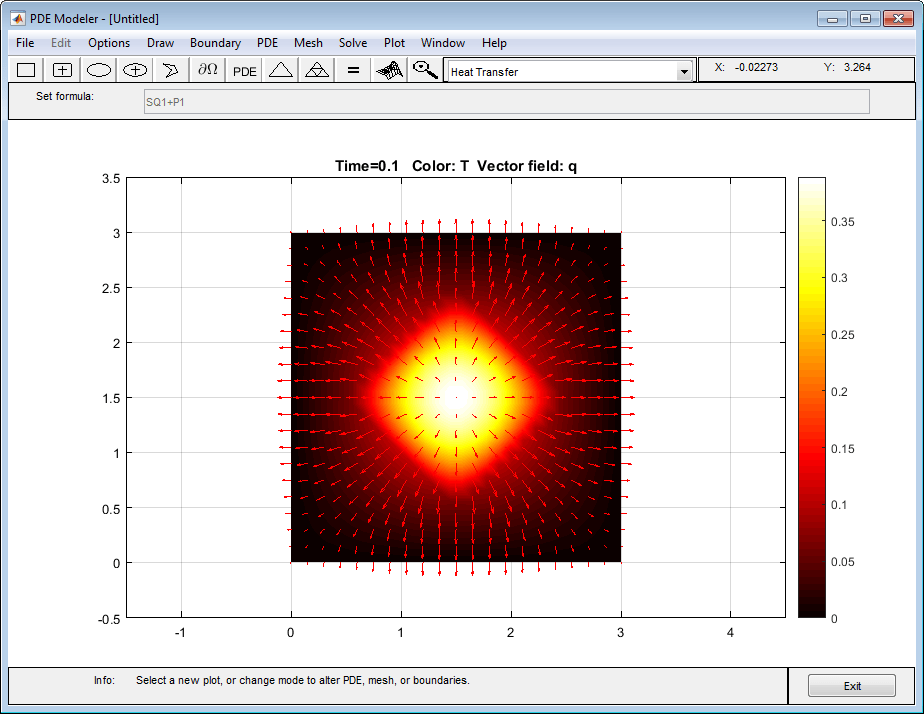
Для второго графика выберите Color и Arrows и установите их значения temperature и heat flux, соответственно.
Изотермические линии
Температура и тепловой поток