Найдите статическое магнитное поле, вызванное обмотками статора, в двухполюсном электродвигателе. Принимая, что двигатель длинный, а конечные эффекты незначительны, можно использовать модель 2-D. Геометрия состоит из трех областей:
Две ферромагнитные части: статор и ротор, выполненные из трансформаторной стали
Воздушный зазор между статором и ротором
Медная катушка якоря, несущая постоянный ток
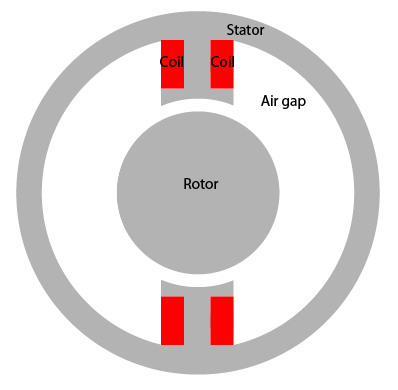
Магнитная проницаемость воздуха и меди близка к магнитной проницаемости вакуума, μ = μ 0. Магнитная проницаемость статора и ротора
где µ max = 5000, µ min = 200 и c = 0,05. Плотность тока J 0 везде, кроме катушки, где это 10 A/m2.
Геометрия задачи делает магнитный векторный потенциал A симметричным относительно оси y и антисимметричным относительно оси x. Поэтому можно ограничить домен x ≥ 0, y ≥ 0, граничным условием по умолчанию
на оси x и граничном условии A = 0 на оси y. Поскольку поле вне двигателя незначительно, можно использовать граничное условие A = 0 на внешнем контуре.
Во-первых, создайте геометрию в приложение PDE Modeler. Геометрия этого электродвигателя представляет собой объединение из пяти кругов и двух прямоугольников. Чтобы нарисовать геометрию, введите следующие команды в MATLAB® Командное окно:
pdecirc(0,0,1,'C1') pdecirc(0,0,0.8,'C2') pdecirc(0,0,0.6,'C3') pdecirc(0,0,0.5,'C4') pdecirc(0,0,0.4,'C5') pderect([-0.2 0.2 0.2 0.9],'R1') pderect([-0.1 0.1 0.2 0.9],'R2') pderect([0 1 0 1],'SQ1')
Уменьшите геометрию до первого квадранта путем пересечения ее с квадратом. Для этого введите (C1+C2+C3+C4+C5+R1+R2)*SQ1 в поле Set formula.
В приложении PDE Modeler экспортируйте матрицу описания геометрии, установите формулу и матрицу пространства имен в рабочее пространство MATLAB, выбрав Export Geometry Description, Set Formula, Labels... из меню Draw.
В Командном Окне MATLAB используйте decsg функция для разложения экспортированной геометрии на минимальные области. Эта команда создает AnalyticGeometry d1 объекта. Постройте график d1.
[d1,bt1] = decsg(gd,sf,ns); pdegplot(d1,'EdgeLabels','on','FaceLabels','on')
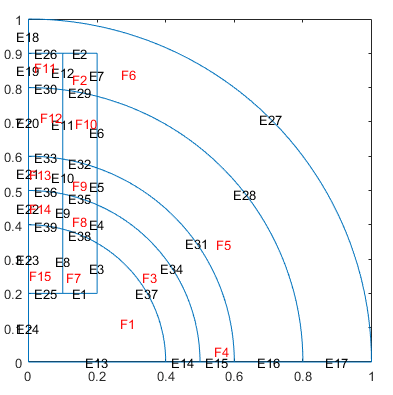
Удалите ненужные ребра с помощью csgdel функция. Укажите ребра, которые нужно удалить, как вектор идентификаторов ребер. Постройте график получившейся геометрии.
[d2,bt2] = csgdel(d1,bt1,[1 3 8 25 7 2 12 26 30 33 4 9 34 10 31]); pdegplot(d2,'EdgeLabels','on','FaceLabels','on')
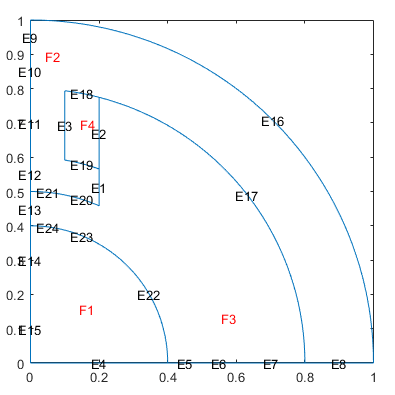
Создайте электромагнитную модель для магнитостатического анализа.
emagmodel = createpde('electromagnetic','magnetostatic');
Включите геометрию в модель.
geometryFromEdges(emagmodel,d2);
Задайте значение вакуумной проницаемости в системе модулей СИ.
emagmodel.VacuumPermeability = 1.2566370614E-6;
Задайте относительную проницаемость воздушного зазора и медной катушки, которые соответствуют граням 3 и 4 геометрии.
electromagneticProperties(emagmodel,'RelativePermeability',1, ... 'Face',[3 4]);
Задайте относительную проницаемость статора и ротора, которая соответствует граням 1 и 2 геометрии.
perm = @(region,state)5000./(1 + 0.05*(state.ux.^2 + ... state.uy.^2)) + 200; electromagneticProperties(emagmodel,'RelativePermeability',perm, ... 'Face',[1 2]);
Задайте плотность тока в катушке.
electromagneticSource(emagmodel,'CurrentDensity',10,'Face',4);
Применить условие нулевого магнитного потенциала ко всем контурам, кроме ребер вдоль оси x. Края вдоль оси x сохраняют граничное условие по умолчанию.
electromagneticBC(emagmodel,'MagneticPotential',0,... 'Edge',[16 9 10 11 12 13 14 15]);
Сгенерируйте mesh.
generateMesh(emagmodel);
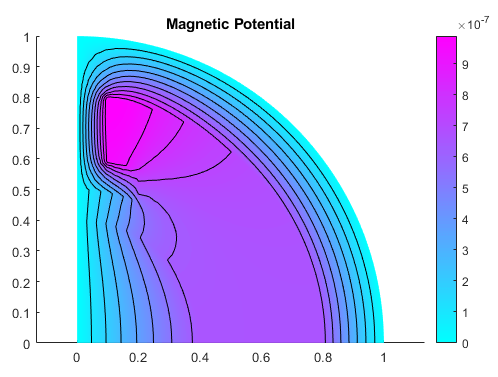
Решите модель и постройте график магнитного потенциала. Используйте Contour параметр для отображения эквипотенциальных линий.
R = solve(emagmodel); pdeplot(emagmodel,'XYData',R.MagneticPotential,'Contour','on') title 'Magnetic Potential'
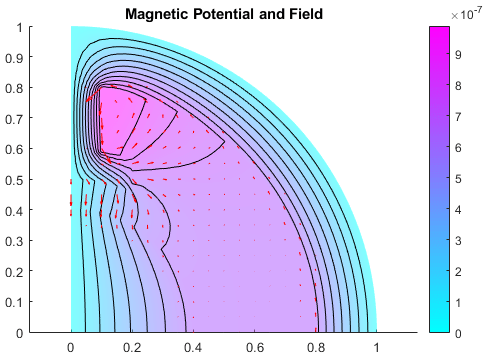
Добавьте данные магнитного поля к графику. Используйте FaceAlpha параметр, чтобы сделать график полей градиента для магнитного поля более видимым.
pdeplot(emagmodel,'XYData',R.MagneticPotential, ... 'FlowData',[R.MagneticField.Hx, ... R.MagneticField.Hy], ... 'Contour','on', ... 'FaceAlpha',0.5) title 'Magnetic Potential and Field'