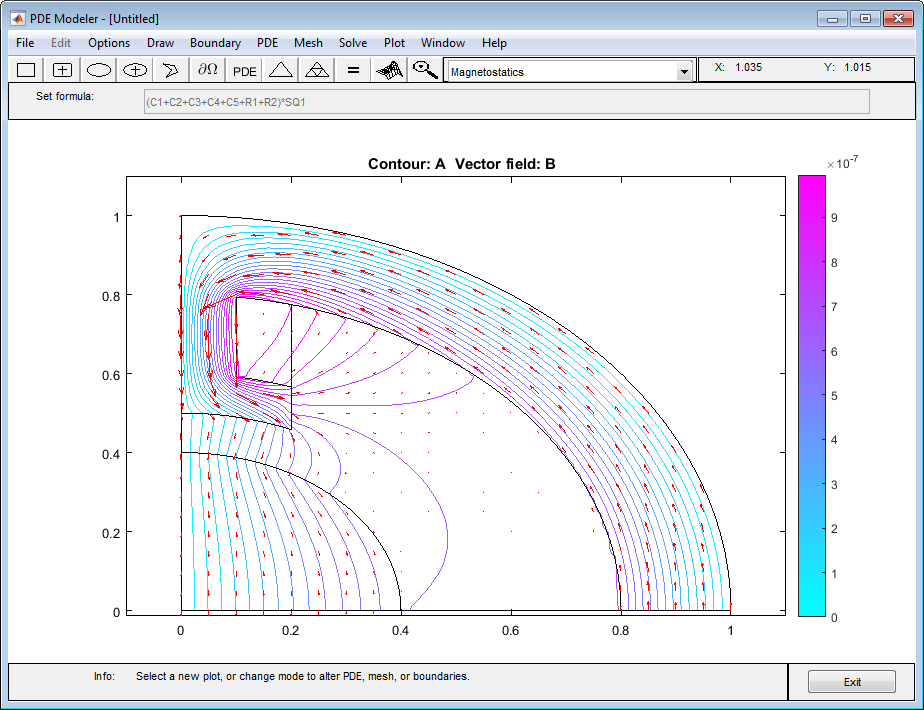
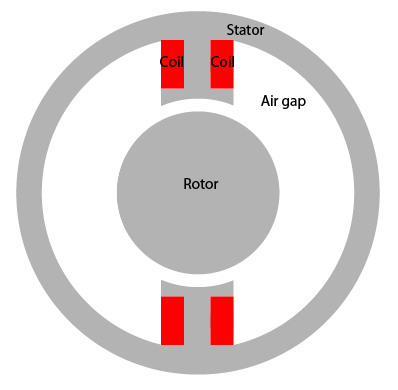
Найдите статическое магнитное поле, вызванное обмотками статора, в двухполюсном электродвигателе. Пример использует приложение PDE Modeler. Принимая, что двигатель длинный, а эффекты конца незначительны, можно использовать модель 2-D. Геометрия состоит из трех областей:
Две ферромагнитные части: статор и ротор (трансформаторная сталь)
Воздушный зазор между статором и ротором
Медная катушка якоря, несущая постоянный ток
Магнитная проницаемость воздуха и меди близка к магнитной проницаемости вакуума, μ 0 = 4 π * 10-7 Ч/м. В этом примере используйте магнитную проницаемость μ = μ 0 для воздушного зазора и медной катушки. Для статора и ротора μ есть
где µ max = 5000, µ min = 200 и c = 0,05. Плотность тока J 0 везде, кроме катушки, где это 10 A/m2.
Геометрия задачи делает магнитный векторный потенциал A симметричным относительно y и антисимметричным относительно x. Поэтому можно ограничить область x ≥ 0, y ≥ 0 с граничным условием Неймана
на оси x и граничном условии Дирихле A = 0 на оси y. Поскольку поле вне двигателя незначительно, можно использовать граничное условие Дирихле A = 0 на внешнем контуре.
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие шаги:
Установите пределы x -оси равными [-1.5 1.5] и пределы y оси [-1 1]. Для этого выберите Options > Axes Limits и установите соответствующие области значений.
Установите режим приложения равным Magnetostatics.
Создайте геометрию. Геометрия этого электродвигателя сложная. Модель представляет собой объединение из пяти кругов и двух прямоугольников. Сокращение до первого квадранта достигается пересечением с квадратом. Чтобы нарисовать геометрию, введите следующие команды в MATLAB® Командное окно:
pdecirc(0,0,1,'C1') pdecirc(0,0,0.8,'C2') pdecirc(0,0,0.6,'C3') pdecirc(0,0,0.5,'C4') pdecirc(0,0,0.4,'C5') pderect([-0.2 0.2 0.2 0.9],'R1') pderect([-0.1 0.1 0.2 0.9],'R2') pderect([0 1 0 1],'SQ1')
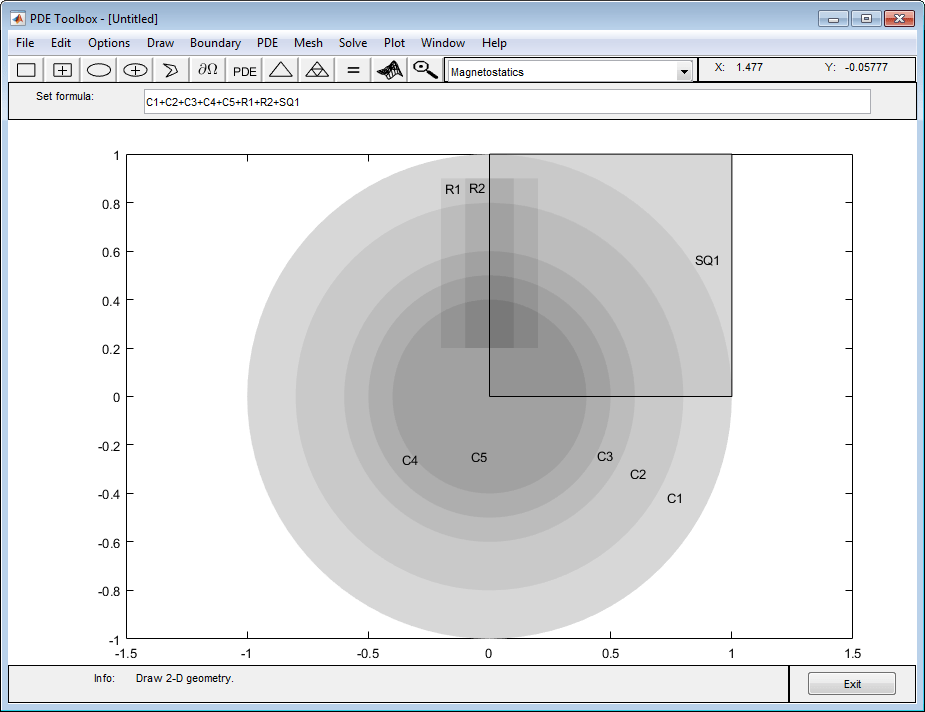
Уменьшите модель до первого квадранта. Для этого введите (C1+C2+C3+C4+C5+R1+R2)*SQ1 в поле Set formula.
Удалите ненужные границы поддомена. Для этого перейдите в граничный режим путем выбора Boundary > Boundary Mode. Используя Shift + нажатие кнопки, выберите границы, а затем выберите Boundary > Remove Subdomain Border, пока геометрия не будет состоять из четырех поддоменов: ротора (поддомен 1), статора (поддомен 2), воздушной щели (поддомен 3) и катушки (поддомен 4). Нумерация ваших поддоменов может различаться. Если вы не видите цифры, выберите Boundary > Show Subdomain Labels.
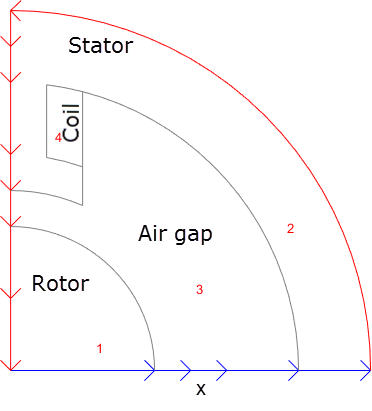
Задайте граничные условия. Для этого выберите контуры вдоль оси x. Выберите Boundary > Specify Boundary Conditions. В получившемся диалоговом окне задайте граничное условие Неймана с g = 0 и q = 0.
Все другие контуры имеют граничное условие Дирихле с h = 1 и r = 0, которое является граничным условием по умолчанию в приложении PDE Modeler.
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Дважды кликните каждый поддомен и задайте следующие коэффициенты:
Катушка: µ = 4*pi*10^(-7) Н/м, J = 10 Утра2.
Статор и ротор: µ = 4*pi*10^(-7)*(5000./(1+0.05*(ux.^2+uy.^2))+200) H/m, где ux.^2+uy.^2 равен |∇<reservedrangesplaceholder0> |2, J = 0 (ток отсутствует).
Воздушная погрешность: µ = 4*pi*10^(-7) Н/м, J = 0.
Инициализируйте mesh путем выбора Mesh > Initialize Mesh.
Выберите нелинейный решатель. Для этого выберите Solve > Parameters и проверьте Use nonlinear solver. Здесь можно также настроить параметр допуска и принять решение использовать адаптивный решатель вместе с нелинейным решателем.
Решить УЧП можно путем выбора Solve > Solve PDE или нажатия кнопки = на панели инструментов.
Постройте график плотности магнитного потока B помощи стрел и эквипотенциальных линий магнитостатического потенциала A используя контурный график. Для этого выберите Plot > Parameters и выберите контур и стрелы графиков в получившемся диалоговом окне. Используя Options > Axes Limits, скорректируйте пределы осей по мере необходимости. Например, используйте флажок Auto.
График показывает, что магнитный поток параллелен эквипотенциальным линиям магнитостатического потенциала.