Задача рассеяния: приложение PDE Modeler

Этот пример показывает, как решить простую задачу рассеяния, где вы вычисляете волны, отраженные квадратным объектом, освещенным падающими волнами, которые идут слева. Этот пример использует приложение PDE Modeler. Для получения информации о программных рабочих процессах смотрите Задачу Рассеяния.

Для этой задачи предположим, что бесконечная горизонтальная мембрана, подвергнутая небольшим вертикальным перемещениям, U. Мембрана закреплена на контуре объекта. Среда однородна, и скорость фазы (скорость распространения) волны, α, постоянна. Волновое уравнение

$\frac{\partial^{2} U}{\partial t^{2}} - α^{2} Δ U = 0$

Решение U является суммой падающей волны V и отраженная волна R:

U = V + R

Когда освещенность является гармонической во времени, можно вычислить поле, решив одну устойчивую задачу. Предположим, что падающая волна является плоской волной, перемещающейся в направлении - x:

$V (x, y, t) = e^{i (- k x - ω t)} = e^{- i k x} e^{- i ω t}$

Отраженная волна может быть разложена на пространственные и временные компоненты:

$R (x, y, t) = r (x, y) e^{- i ω t}$

Теперь можно переписать волновое уравнение как уравнение Гельмгольца для пространственного компонента отраженной волны с числом волн k = ω/ α:

-В r - k²r = 0

Граничное условие Дирихле для контура объекта - U = 0, или в терминах падающих и отраженных волн, R = - V. Для гармонического решения во времени и падающей волны, перемещающейся в направлении - x, можно записать это граничное условие следующим образом:

$r (x, y) = - e^{- i k x}$

Отраженная волна R перемещается наружу от объекта. Условие на внешнем вычислительном контуре должно позволить волнам проходить без отражения. Такие условия обычно называют неповторяющимися. Как $| \vec{x} |$ приближается к бесконечности, R приблизительно удовлетворяет уравнению односторонней волны

$\frac{\partial R}{\partial t} + α \vec{ξ} \cdot \nabla R = 0$

Это уравнение рассматривает только волны, движущиеся в положительном ξ -направлении. Здесь ξ - радиальное расстояние от объекта. С помощью гармонического во времени решения это уравнение превращается в обобщенное граничное условие Неймана

$\vec{ξ} \cdot \nabla r = i k r$

Чтобы решить проблему рассеяния в приложении PDE Modeler, выполните следующие шаги:

Откройте приложение PDE Modeler при помощи pdeModeler команда.
Установите x предел оси равным [0.1 1.5] и предел по оси y, равный [0 1]. Для этого выберите Options > Axes Limits и установите соответствующие области значений.
Отображение линий сетки. Для этого:
1. Выберите Options > Grid Spacing и снимите флажки Auto.
2. Введите X-axis linear spacing следующим 0.1:0.05:1.5 и Y-axis linear spacing как 0:0.05:1.
3. Выберите Options > Grid.
Выровнять новые формы по линиям сетки можно путем выбора Options > Snap.
Нарисуйте квадрат со сторонами длины 0,1 и центром в [0.8 0.5]. Для этого сначала нажмите кнопку. Затем щелкните правой кнопкой мыши источник и перетащите мышью, чтобы нарисовать квадрат. Щелчок правой кнопкой мыши ограничивает рисуемую форму так, чтобы она была квадратной, а не прямоугольной. Если квадрат не идеальный квадрат, дважды кликните его. В получившемся диалоговом окне задайте точное расположение нижнего левого угла и длину стороны.
Поверните квадрат на 45 степени. Для этого выберите Draw > Rotate... и введите 45 в получившемся диалоговом окне. Повернутый квадрат представляет освещенный объект.
Нарисуйте окружность с радиусом 0,45 и центром в [0.8 0.5]. Для этого сначала нажмите кнопку. Затем щелкните правой кнопкой мыши источник и перетащите мышью, чтобы нарисовать круг. Щелчок правой кнопкой мыши ограничивает рисуемую форму так, чтобы она была окружностью, а не эллипсом. Если окружность не является идеальной единичной окружностью, дважды кликните ее. В получившемся диалоговом окне задайте точное центральное положение и радиус окружности.
Моделируйте геометрию путем ввода C1-SQ1 в поле Set formula.
Проверьте, что в прикладном режиме задано значение Generic Scalar.
Задайте граничные условия. Для этого перейдите в граничный режим путем выбора Boundary > Boundary Mode. Используйте команду Shift + нажатие кнопки, чтобы выбрать несколько контуры. Затем выберите Boundary > Specify Boundary Conditions.
- Для периметра окружности граничным условием является граничное условие Неймана с q = -ik, где номер волны k = 60 соответствует длине волны около 0,1 модули. Введите g = 0 и q = -60*i.
- Для периметра квадрата граничным условием является граничное условие Дирихле:
  $r = - v (x, y) = - e^{i k \vec{a} \cdot \vec{x}}$
  В этой задаче, поскольку отраженная волна перемещается в направлении - x, граничное условие r = -e^–ikx. Введите h = 1 и r = -exp(-i*60*x).
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Уравнение Гельмгольца является волновым уравнением, но в Partial Differential Equation Toolbox™ можно рассматривать его как эллиптическое уравнение с a = -k². Задайте c = 1, a = -3600, и f = 0.
Инициализируйте mesh путем выбора Mesh > Initialize Mesh.
Для достаточной точности вам нужно около 10 конечных элементов на длину волны. Внешний контур должна располагаться в нескольких диаметрах от самого объекта. Уточнить mesh можно путем выбора Mesh > Refine Mesh. Уточните mesh еще два раза, чтобы получить необходимое разрешение.
Решить УЧП можно путем выбора Solve > Solve PDE или нажатия кнопки = на панели инструментов.
Решение комплексное. При построении графика решения вы получаете предупреждающее сообщение.
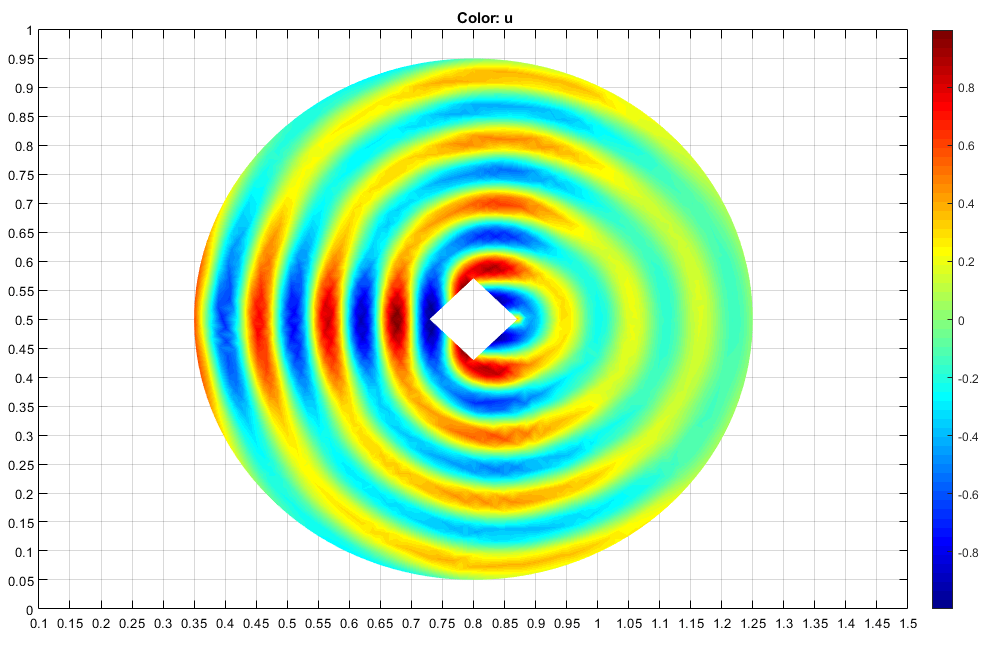
Постройте график отраженных волн. Измените палитру на jet путем выбора Plot > Parameters и последующего выбора jet из раскрывающегося меню Colormap.
Анимируйте решение для зависящего от времени волнового уравнения. Для этого:
1. Экспорт данных сетки и решения в MATLAB^® рабочей области путем выбора Mesh > Export Mesh и Solve > Export Solution, соответственно.
2. Введите следующие команды в Командном Окне MATLAB.
```
figure
maxu = max(abs(u)); 
m = 10;
for j = 1:m, 
   uu = real(exp(-j*2*pi/10*sqrt(-1))*u); 
   pdeplot(p,e,t,'XYData',uu,'ColorBar','off','Mesh','off');
   colormap(jet)
   caxis([-maxu maxu]);
   axis tight
   ax = gca;
   ax.DataAspectRatio = [1 1 1]; 
   axis off
   M(:,j) = getframe; 
 end
movie(M);
```

Документация

Задача рассеяния: приложение PDE Modeler

Partial Differential Equation Toolbox производными

Поддержка