Чтобы задать параметры для решения УЧП, выберите Parameters из меню Solve. Набор параметров решения отличается в зависимости от типа PDE. После настройки параметров решите УЧП, выбрав Solve PDE из меню Solve или нажав![]() кнопку.
кнопку.
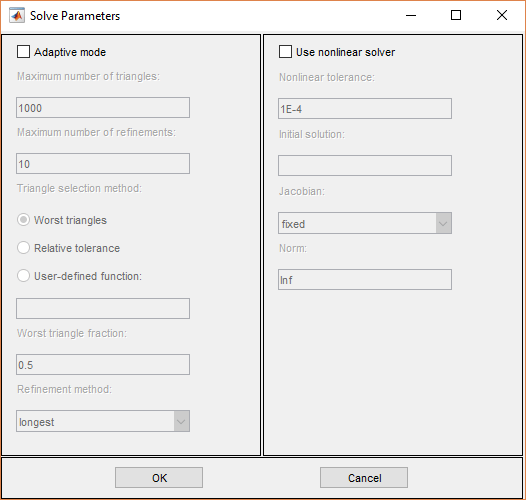
По умолчанию никакие конкретные параметры решения не используются, и эллиптические PDE решаются с помощью базового эллиптического решателя assempde. Опционально адаптивный генератор сетки и решатель adaptmesh может использоваться. Для адаптивного режима доступны следующие параметры:
Adaptive mode. Включите/отключите адаптивный режим.
Maximum number of triangles. Максимально допустимое количество новых треугольников (может быть установлено на Inf). Значение по умолчанию вычисляется на основе текущего mesh.
Maximum number of refinements. Максимальное количество попыток последовательных уточнений.
Triangle selection method. Существует два метода выбора треугольника, описанных ниже. Вы также можете предоставить свою собственную функцию.
Worst triangles. Этот метод выбирает все треугольники, которые хуже части значения худшего треугольника (по умолчанию: 0,5).
Relative tolerance. Этот метод выбирает треугольники с помощью критерия относительной погрешности (по умолчанию: 1E-3).
User-defined function. Введите имя пользовательского метода выбора треугольника. Смотрите уравнение Пуассона с источником точек и адаптивное уточнение сетки для примера пользовательского метода выбора треугольника.
Function parameter. Параметр функции позволяет подстройку методов выбора треугольника. Для метода наихудшего треугольника (pdeadworst), это часть наихудшего значения, которая используется, чтобы определить, какие треугольники следует уточнить. Для метода относительной погрешности это параметр допуска, который управляет тем, насколько хорошо решение подходит для УЧП.
Refinement method. Можно regular или longest. См. раздел «Задание параметров сетки» в приложении PDE Modeler.
Если задача нелинейна, то есть параметры в УЧП напрямую зависят от решения u, должен использоваться нелинейный решатель. Используются следующие параметры:
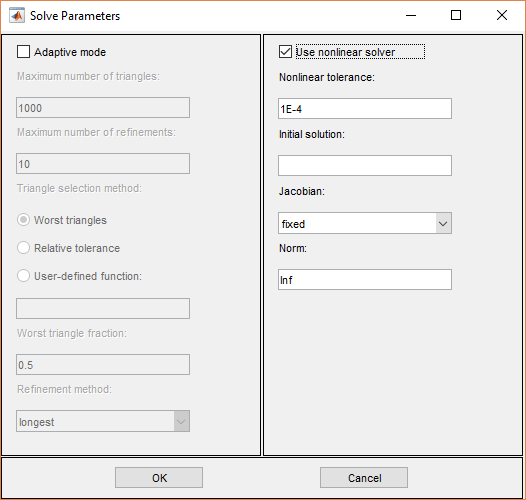
Use nonlinear solver. Включите/отключите нелинейный решатель.
Nonlinear tolerance. Параметр допуска для нелинейного решателя.
Initial solution. Начальное предположение. Может быть константой или функцией x и y, заданной как MATLAB® выражение, которое может быть вычислено на узлах текущего mesh.
Примеры: 1, и exp(x.*y). Необязательный параметр, по умолчанию равный нулю.
Jacobian. Якобианский метод приближения: fixed (по умолчанию), итерация фиксированной точки, lumped, «комкнутое» (диагональное) приближение, или full, полный якобиан.
Norm. Тип нормы, используемой для вычисления невязки. Введите как energy для энергетической нормы или как действительной скалярной p, чтобы задать l p норму. Значение по умолчанию является Inf, бесконечность (максимальная) норма.
Примечание
Адаптивный режим и нелинейный решатель могут использоваться вместе.
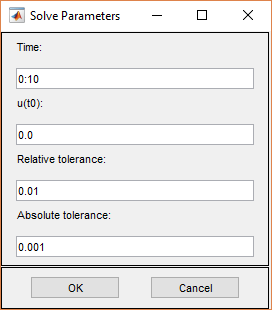
Параметрами решения для параболических PDE являются:
Time. Вектор MATLAB времени, в которые должно быть сгенерировано решение параболического УЧП. Соответствующий временной интервал зависит от динамики задачи.
Примеры: 0:10, и logspace(-2,0,20)
u(t0). Начальное значение u (t 0) для параболического УЧП задачи Начальное значение может быть константой или вектором-столбцом значений на узлах текущего mesh.
Relative tolerance. Относительная погрешность для решателя ОДУ, который используется для решения зависящей от времени части параболической задачи УЧП.
Absolute tolerance. Абсолютная погрешность для решателя ОДУ, который используется для решения зависящей от времени части параболической задачи УЧП.
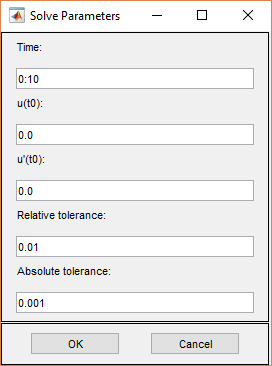
Параметрами решения для гиперболических PDE являются:
Time. Вектор MATLAB времени, в которые должно быть сгенерировано решение гиперболического УЧП. Соответствующий временной интервал зависит от динамики задачи.
Примеры: 0:10, и logspace(-2,0,20).
u(t0). Начальное значение u (t 0) для гиперболического УЧП задачи. Начальное значение может быть константой или вектором-столбцом значений на узлах текущего mesh.
u'(t0). Начальное значение (t 0) для гиперболического УЧП задачи. Можно использовать те же форматы, что и для u(t0).
Relative tolerance. Относительная погрешность для решателя ОДУ, который используется для решения зависящей от времени части гиперболической задачи УЧП.
Absolute tolerance. Абсолютная погрешность для решателя ОДУ, который используется для решения зависящей от времени части гиперболической задачи УЧП.
Для собственного значения PDE единственным параметром решения является Eigenvalue search range, двухэлементный вектор, определяющий интервал на вещественной оси как область значений поиска собственных значений. Левая сторона может быть -Inf.
Примеры: [0 100], [-Inf 50]
Перед решением нелинейного эллиптического УЧП в приложении PDE Modeler выберите Solve Parameters. Затем выберите Use nonlinear solver и нажмите OK.