В этом примере показано, как вычислить смещения u и v и эффективное напряжение фон Мизеса для стального диска, который зажат вдоль прямоугольной вставки в левом нижнем углу и натянут на скругленный разрез в правом верхнем углу. В примере используется PDE Modeler app.Приложение также позволяет вам вычислять и визуализировать другие свойства, такие как x - и y - направляющие напряжения и напряжения сдвига.
Рассмотрим стальной диск, который зажимается вдоль прямоугольной вставки в левом нижнем углу и натягивается на скругленный разрез в правом верхнем углу. Все остальные стороны свободны. Стальной диск обладает следующими свойствами:
Размерности 1 m-1 m-by 0,001 м;
Вставка 1/3 на 1/3 м
Округлый разрез проходит от (2/3, 1) до (1, 2/3)
Модуль Янга: 196· 103 (МН/м2)
Коэффициент Пуассона: 0,31.
Изогнутый контур подвергается внешней нормальной нагрузке 500 Н/м. Чтобы задать поверхностную тягу, разделите нагрузку на толщину (0,001 м). Таким образом, поверхностная тяга составляет 0,5 МН/м2. Сила, модуль в этом примере, является MN.
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие шаги:
Нарисуйте многоугольник с углами (0 1), (2/3,1), (1,2/3), (1,0), (1/3,0), (1/3,1/3), (0,1/3) и окружностью с центром (2/3, 2/3) и радиусом 1/3.
pdepoly([0 2/3 1 1 1/3 1/3 0],[1 1 2/3 0 0 1/3 1/3]) pdecirc(2/3,2/3,1/3)
Установите x предел оси равным [-0.5 1.5] и y предел оси [0 1.2]. Для этого выберите Options > Axes Limits и установите соответствующие области значений.
Моделируйте геометрию путем ввода P1+C1 в поле Set formula.
Установите режим приложения равным Structural Mechanics, Plane Stress.
Удалите все границы поддомена. Для этого перейдите в граничный режим путем выбора Boundary > Boundary Mode. Затем выберите Boundary > Remove All Subdomain Borders.
Отображение меток ребра путем выбора Boundary > Show Edge Labels.
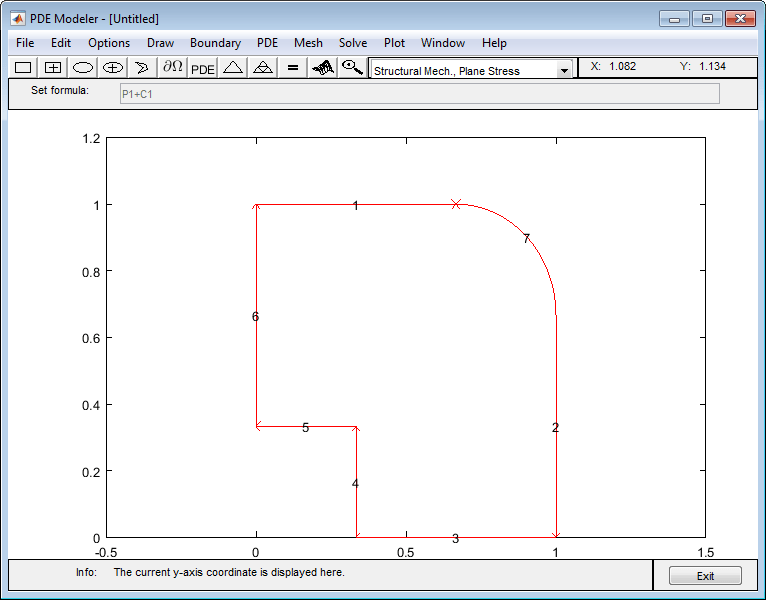
Задайте граничные условия. Для этого выберите Boundary > Specify Boundary Conditions.
Для удобства сначала задайте граничное условие Неймана g1 = g2 = 0, q11 = q12 = q21 = q22 = 0 (без нормального напряжения) для всех контуров. Используйте команду Edit > Select All, чтобы выбрать все контуры.
Для двух зажатых контуров у вставки в нижнем левом углу (ребра 4 и 5) задайте граничное условие Дирихле с нулевыми перемещениями: h11 = 1, h12 = 0, h21 = 0, h22 = 1, r1 = 0, r2 = 0. Используйте команду Shift + нажатие кнопки, чтобы выбрать несколько контуры.
Для скругленного выреза (ребро 7) задайте граничное условие Неймана: g1 = 0.5*nx, g2 = 0.5*ny, q11 = q12 = q21 = q22 = 0.
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Задайте E = 196E3 и nu = 0.31. Материал однороден, поэтому те же самые значения E и nu применить ко всему 2-D области. Поскольку объемных сил нет, задайте Kx = Ky = 0. Эллиптический тип PDE для плоского напряжения не использует плотность, поэтому можно задать любое значение. Для примера задайте pho = 0.
Инициализируйте mesh путем выбора Mesh > Initialize Mesh. Уточнить mesh можно путем выбора Mesh > Refine Mesh.
Уточнение mesh в областях, где градиент решения (напряжение) является большим. Для этого выберите Solve > Parameters. В получившемся диалоговом окне выберите Adaptive mode. Используйте опции адаптации по умолчанию: Worst triangles метод выбора треугольника с Worst triangle fraction, установленной на 0.5.
Решить УЧП можно путем выбора Solve > Solve PDE или нажатия кнопки = на панели инструментов.
Постройте график эффективного напряжения фон Мизеса с помощью цвета. Постройте график векторного поля (u, v) с помощью деформированного mesh. Для этого:
Выберите Plot > Parameters.
В получившемся диалоговом окне выберите опции Color и Deformed mesh. Выберите von Mises из раскрывающегося меню Color. Выберите Show Mesh, чтобы наблюдать уточнённый mesh в больших областях напряжений.
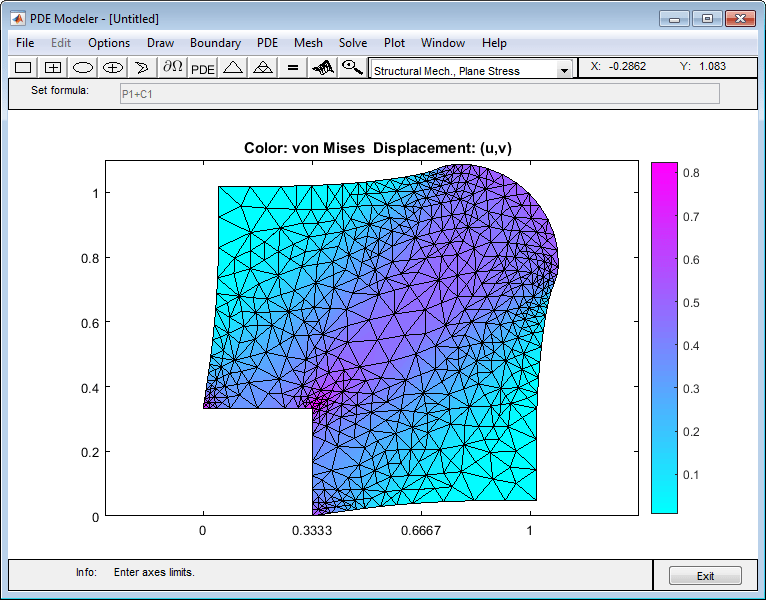
Выбрав другие опции из выпадающего меню Color, можно визуализировать различные свойства напряжения и деформации, такие как x- и y- направления и напряжения, напряжение сдвига и основные напряжения и деформации. Можно также построить графики комбинаций скаляра и вектора свойств с помощью цвета, высоты, стрелы векторного поля и перемещений на 3-D графике, чтобы представлять различные свойства.