Волновое уравнение в квадратной области: приложение PDE Modeler
Этот пример показывает, как решить волновое уравнение для поперечных вибраций мембраны на квадрате. Мембрана закреплена с левой и правой сторон и свободна с верхней и нижней сторон. Этот пример использует PDE Modeler, приложение. Для программного рабочего процесса смотрите Волновое уравнение в квадратной области.
Волновое уравнение является гиперболическим УЧП:
Чтобы решить эту проблему в приложении PDE Modeler, выполните следующие шаги:
Откройте приложение PDE Modeler при помощи
pdeModelerкоманда.Отобразить линии сетки можно путем выбора Options > Grid.
Выровнять новые формы по линиям сетки можно путем выбора Options > Snap.
Нарисуйте квадрат с углами в (-1, -1), (-1,1), (1,1) и (1, -1). Для этого сначала нажмите
кнопку. Затем щелкните один из углов правой кнопкой мыши и перетащите мышью, чтобы нарисовать квадрат. Правая кнопка мыши ограничивает форму, которую вы рисуете, квадратной, а не прямоугольником.Вы также можете использовать
pderectфункция:pderect([-1 1 -1 1])
Проверьте, что в прикладном режиме задано Generic Scalar.
Задайте граничные условия. Для этого перейдите в граничный режим нажатием
кнопки или выбором Boundary > Boundary Mode. Выберите левые и правые контуры. Затем выберите Boundary > Specify Boundary Conditions и задайте граничное условие Дирихле u = 0. Это граничное условие является условием по умолчанию (h = 1,r = 0), так что менять его не нужно.Для нижней и верхней границ установите граничное условие Неймана ∂ u/ ∂ n = 0. Для этого
установите g = 0,q = 0.Задайте коэффициенты, выбрав PDE PDE Specification или нажав кнопку PDE на панели инструментов. Выберите тип Hyperbolic УЧП и задайте
c = 1,a = 0,f = 0, иd = 1.Инициализируйте mesh путем выбора Mesh > Initialize Mesh. Уточнить mesh можно путем выбора Mesh > Refine Mesh.
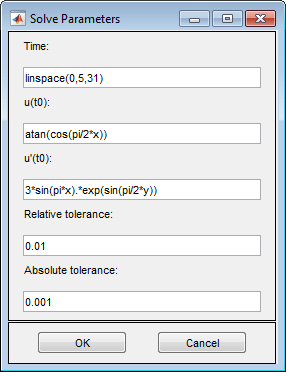
Установите время решения. Для этого выберите Solve > Parameters. Создайте линейно разнесенные временные векторы от 0 до 5 секунд путем установки времени решения на
linspace(0,5,31).В том же диалоговом окне задайте начальные условия для волнового уравнения. Для хорошо проведенного решения начальные значения должны совпадать с граничными условиями. Если начальное время t = 0, то следующие начальные значения, которые удовлетворяют граничным условиям:
atan(cos(pi/2*x))дляu(0)и3*sin(pi*x).*exp(sin(pi/2*y))для ∂ u/ ∂ t,Обратная тангенциальная функция и экспоненциальная функция вводят больше режимов в решение.
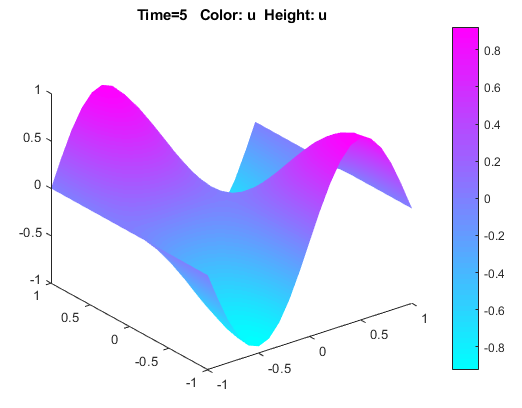
Решить УЧП можно путем выбора Solve > Solve PDE или нажатия кнопки = на панели инструментов. Приложение решает уравнение тепла в моменты времени от 0 до 5 секунд и отображает результат в конце временного интервала.
Визуализируйте решение как 3-D статические и анимированные графики. Для этого:
Выберите Plot > Parameters.
В получившемся диалоговом окне выберите опции Color и Height (3-D plot).
Чтобы визуализировать динамическое поведение волны, выберите Animation в том же диалоговом окне. Если прогресс анимации слишком медленный, выберите опцию Plot in x-y grid. Сетка x - y может значительно ускорить процесс анимации.
