Exponenta Banner

Детекторы постоянной частоты ложных предупреждений (CFAR)

Скорость ложного оповещения для детекторов CFAR

Открыть скрипт

В среде Неймана-Пирсона вероятность обнаружения максимизируется при условии ограничения, что вероятность ложного предупреждения не превышает заданный уровень. Вероятность ложного предупреждения зависит от отклонения шума. Поэтому, чтобы вычислить вероятность ложного предупреждения, необходимо сначала оценить отклонение шума. Если отклонение шума изменяется, необходимо настроить порог, чтобы поддерживать постоянную частоту ложных предупреждений. Постоянные детекторы частоты ложных предупреждений реализуют адаптивные процедуры, которые позволяют вам обновлять пороговый уровень своего теста, когда изменяется мощность помех.

Чтобы мотивировать необходимость адаптивной процедуры, примите простой тест двоичной гипотезы, где вы должны решить между гипотезами отсутствия сигнала и присутствия сигнала для одной выборки. Сигнал имеет амплитуду 4, и шум является нулевым гауссовым с единичным отклонением.

$$H_{0}: x = w,$$ \quad $$w \sim N(0,1)$$

$$H_{1}: x = 4 + w$$

Сначала установите скорость ложного предупреждения 0,001 и определите порог.

T = npwgnthresh(1e-3,1,'real');
threshold = sqrt(db2pow(T))

threshold =

    3.0902

Проверяйте, что этот порог приводит к желаемой вероятности ложного предупреждения, а затем вычислите вероятность обнаружения.

pfa = 0.5*erfc(threshold/sqrt(2))
pd = 0.5*erfc((threshold-4)/sqrt(2))

pfa =

   1.0000e-03


pd =

    0.8185

Затем примите, что степень шума увеличивается на 6,02 дБ, удваивая отклонение шума. Если ваш детектор не адаптируется к этому увеличению отклонения путем определения нового порога, ваша частота ложных предупреждений значительно увеличивается.

pfa = 0.5*erfc(threshold/2)

pfa =

    0.0144

Следующий рисунок показывает эффект увеличения отклонения шума на вероятности ложного предупреждения для фиксированного порога.

noisevar = 1:0.1:10;
noisepower = 10*log10(noisevar);
pfa = 0.5*erfc(threshold./sqrt(2*noisevar));
semilogy(noisepower,pfa./1e-3)
grid on
title('Increase in P_{FA} due to Noise Variance')
ylabel('Increase in P_{FA} (Orders of Magnitude)')
xlabel('Noise Power Increase (dB)')

Среднесуточный CFAR-детектор

CFAR-детектор, усредняющий ячейку, оценивает отклонение шума для интересующей камеры области значений или тестируемой камеры путем анализа данных из соседних камер области значений, обозначенных как обучающие камеры. Шумовые характеристики в обучающих камерах приняты идентичными шумовым характеристикам в тестируемой камере (CUT).

Это предположение является ключевым в обосновании использования обучающих камер для оценки отклонения шума в CUT. Кроме того, среднесрочный CFAR-детектор принимает, что обучающие камеры не содержат никаких сигналов от целей. Таким образом, данные в обучающих камерах приняты состоящими только из шума.

Чтобы сделать эти предположения реалистичными:

  • Предпочтительно иметь некоторое количество буфера или guard cells между CUT и обучающими камерами. Буфер, предоставленный защитными камерами, защищает от утечки сигнала в обучающие камеры и отрицательно влияет на оценку отклонения шума.

  • Обучающие камеры не должны представлять камеры области значений, слишком удаленные в области значений от CUT, как показано на следующем рисунке.

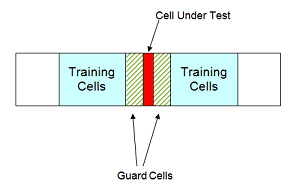
Оптимальный оценщик для отклонения шума зависит от распределительных допущений и типа детектора. Предположим следующее:

  1. Вы используете детектор квадратного закона.

  2. У вас есть Гауссова, комплексная, случайная переменная (RV) с независимыми вещественными и мнимыми частями.

  3. Каждая из вещественных и мнимых частей имеет средний нуль и отклонение, равную2/2.

    Примечание

    Если вы обозначаете это RV на Z = U + jV, квадратная величина |Z|2 следует экспоненциальному распределению со средним2.

Если выборки в обучающих камерах являются квадратными величинами таких сложных Гауссовых RV, можно использовать среднее значение выборки в качестве оценщика отклонения шума.

Чтобы реализовать среднее по ячейкам обнаружение CFAR, используйте phased.CFARDetector. Можно настроить характеристики детектора, такие как количество обучающих камер и защитных камер, и вероятность ложного предупреждения.

Адаптация детектора CFAR к шумным входным данным

Открыть Live Script

В этом примере показано, как создать детектор CFAR и проверить его способность адаптироваться к статистике входных данных. Тест использует испытания только для шума. При помощи детектора квадратного закона по умолчанию можно определить, насколько близка эмпирическая частота ложных предупреждений к желаемой вероятности ложных предупреждений.

Примечание.Этот пример выполняется только в R2016b или более поздней версии. Если вы используете более ранний релиз, замените каждый вызов функции на эквивалентный step синтаксис. Для примера замените myObject(x) с step(myObject,x).

Создайте объект детектора CFAR с двумя защитными камерами, 20 обучающими камерами и вероятностью ложного предупреждения 0,001. По умолчанию этот объект принимает детектор квадратного закона без импульсного интегрирования.

detector = phased.CFARDetector('NumGuardCells',2,...
    'NumTrainingCells',20,'ProbabilityFalseAlarm',1e-3);

На каждой стороне тестируемой камеры (CUT) имеется 10 обучающих камеры и по 1 защитной камере. Установите индекс CUT равным 12.

CUTidx = 12;

Инициализируйте генератор случайных чисел для воспроизводимого набора входных данных.

rng(1000);

Установите отклонение шума равным 0,25. Это значение соответствует приблизительному ОСШ -6 дБ. Сгенерируйте 23 на 10000 матрицу комплексных, белых гауссовских rv с заданным отклонением. Каждая строка матрицы представляет 10 000 исследований Монте-Карло для одной камеры.

Ntrials = 1e4;
variance = 0.25;
Ncells = 23;
inputdata = sqrt(variance/2)*(randn(Ncells,Ntrials)+1j*randn(Ncells,Ntrials));

Поскольку в примере реализован детектор квадратного закона, возьмите квадратные величины элементов в матрице данных.

Z = abs(inputdata).^2;

Предоставьте выход от оператора квадратного закона и индекс тестируемой камеры детектору CFAR.

Z_detect = detector(Z,CUTidx);

Выход, Z_detect, является логическим вектором с 10000 элементами. Суммируйте элементы в Z_detect и разделите на общее количество испытаний, чтобы получить эмпирическую частоту ложных предупреждений.

pfa = sum(Z_detect)/Ntrials
pfa = 0.0013

Эмпирическая частота ложных предупреждений составляет 0,0013, что тесно соответствует желаемой частоте ложных предупреждений 0,001.

Расширения CFAR-детектора, усредняющего ячейку

Алгоритм усреднения ячеек для CFAR-детектора хорошо работает во многих ситуациях, но не во всех. Для примера, когда цели тесно расположены, камерой среднее может заставить сильную цель замаскировать слабую цель рядом. The phased.CFARDetector Системная object™ поддерживает следующие алгоритмы обнаружения CFAR.

АлгоритмТипичное использование
CFAR со средним количеством ячеекБольшинство ситуаций
Наибольшее среднее значение CFAR для ячеекКогда важно избегать ложных предупреждений на краю загромождения
CFAR с наименьшим средним значением ячейкиКогда цели тесно расположены
Статистика порядка CFARКомпромисс между самым большим и самым маленьким средним значением камеры

Вероятность обнаружения для CFAR-детектора

Открыть Live Script

Этот пример показывает, как сравнить вероятность обнаружения, полученную из двух алгоритмов CFAR. В этом сценарии алгоритм статистики порядка обнаруживает цель, которую алгоритм усреднения ячеек не обнаруживает.

Примечание.Этот пример выполняется только в R2016b или более поздней версии. Если вы используете более ранний релиз, замените каждый вызов функции на эквивалентный step синтаксис. Для примера замените myObject(x) с step(myObject,x).

Создайте детектор CFAR, который использует усредненный по ячейкам алгоритм CFAR.

Ntraining = 10;
Nguard = 2;
Pfa_goal = 0.01;
detector = phased.CFARDetector('Method','CA',...
    'NumTrainingCells',Ntraining,'NumGuardCells',Nguard,...
    'ProbabilityFalseAlarm',Pfa_goal);

Детектор имеет 2 защитные камеры, 10 обучающих камеры и вероятность ложного предупреждения 0,01. Этот объект принимает детектор квадратного закона без импульсного интегрирования.

Сгенерируйте вектор входных данных на основе комплексной белой Гауссовой случайной переменной.

Ncells = 23;
Ntrials = 100000;
inputdata = 1/sqrt(2)*(randn(Ncells,Ntrials) + ...
    1i*randn(Ncells,Ntrials));

В входных данных замените строки 8 и 12, чтобы симулировать две цели, чтобы детектор CFAR обнаружил.

inputdata(8,:) = 3*exp(1i*2*pi*rand);
inputdata(12,:) = 9*exp(1i*2*pi*rand);

Поскольку в примере реализован детектор квадратного закона, возьмите квадратные величины элементов в векторе входных данных.

Z = abs(inputdata).^2;

Выполните обнаружение на строках с 8 по 12.

Z_detect = detector(Z,8:12);

The Z_detect матрица имеет пять строк. Первая и последняя строки соответствуют моделируемым целям. Три средние строки соответствуют шуму.

Вычислите вероятность обнаружения двух целей. Кроме того, оцените вероятность ложного предупреждения, используя строки только для шума.

Pd_1 = sum(Z_detect(1,:))/Ntrials
Pd_1 = 0

Pd_2 = sum(Z_detect(end,:))/Ntrials
Pd_2 = 1

Pfa = max(sum(Z_detect(2:end-1,:),2)/Ntrials)
Pfa = 6.0000e-05

The 0 значение Pd_1 указывает, что этот детектор не обнаруживает первую цель.

Измените детектор CFAR, чтобы он использовал статистический алгоритм CFAR порядка с рангом 5.

release(detector);
detector.Method = 'OS';
detector.Rank = 5;

Повторите обнаружение и расчеты вероятностей.

Z_detect = detector(Z,8:12);
Pd_1 = sum(Z_detect(1,:))/Ntrials
Pd_1 = 0.5820

Pd_2 = sum(Z_detect(end,:))/Ntrials
Pd_2 = 1

Pfa = max(sum(Z_detect(2:end-1,:),2)/Ntrials)
Pfa = 0.0066

Используя алгоритм статистики порядка вместо алгоритма усреднения ячеек, детектор обнаруживает первую цель примерно в 58% испытаний.

Документация по Phased Array System Toolbox

Поддержка