Двухлучевой канал распространения является следующим шагом вверх по сложности от канала свободного пространства и является простейшим случаем многолучевого окружения распространения. Канал свободного пространства моделирует прямолинейный путь наблюдения от точки 1 до точки 2. В двухлучевом канале среда задается как однородная, изотропная среда с отражающим планарным контуром. Значение контура всегда устанавливается на z = 0. Существует не более двух лучей, распространяющихся от точки 1 до точки 2. Первый путь луча распространяется вдоль того же пути видимости, что и в канале свободного пространства (см. phased.FreeSpace Системный object™). Линейный путь часто называют прямой путь. Второй луч отражается вне контура перед распространением в точку 2. Согласно Закону Отражения, угол отражения равен углу падения. В ближних симуляциях, таких как сотовые коммуникационные системы и автомобильные радары, можно предположить, что отражающая поверхность, земля или поверхность океана, плоская.
Рисунок иллюстрирует два пути распространения. Из исходной позиции, ss и позиции приемника, sr, можно вычислить углы прихода обоих путей, θ′los и θ′rp. Углы прихода являются углами повышения и азимута поступающего излучения относительно локальной системы координат. В этом случае локальная система координат совпадает с глобальной системой координат. Можно также вычислить углы передачи, θlos и θrp. В глобальных координатах угол отражения на контуре совпадает с углами θrp и θ′rp. Угол отражения важно знать, когда вы используете зависящие от угла данные отражений и потерь. Можно определить угол отражения при помощи rangeangle функция и установка ссылочных осей в глобальную систему координат. Общая длина пути для линии визирования показана на рисунке по Rlos, которая равна геометрическому расстоянию между источником и приемником. Общая длина пути для отраженного пути Rrp= R1 + R2. Количественный L является наземной областью значений между источником и приемником.
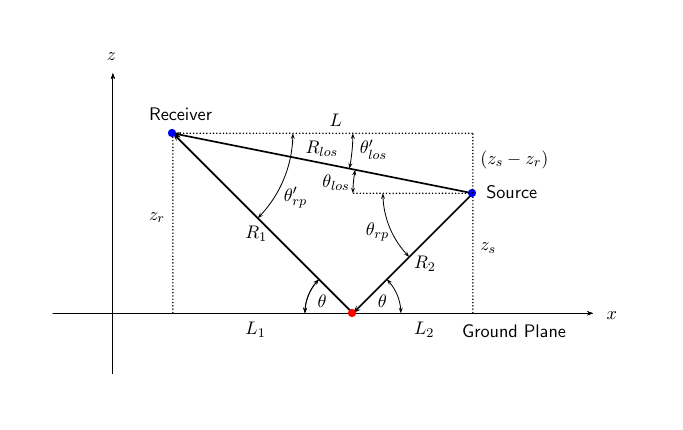
Можно легко вывести точные формулы для длин и углов пути с точки зрения области значений земли и высот объектов в глобальной системе координат.