Отверстие переменного сечения в изотермической аксиально-поршневой машине
Simscape/Жидкости/Изотермическая жидкость/Насосы и двигатели/Вспомогательные компоненты
Блок Клапана Отверстие Диска (IL) моделирует отверстие в форме полумесяца между движущимися поршнями и насосом в аксиально-поршневой машине. Вращающиеся поршни периодически соединяются с входным или выходным отверстием насоса через диафрагму. Можно соединить два блока клапана диска с каждым цилиндром аксиально-поршневого насоса, чтобы представлять входное отверстие насоса и выходные пазы.
Вращающийся цилиндр с одним пазом полумесяца соединен с входным отверстием насоса в порте A и выходным отверстием насоса в порту B. Эти точки соединяются с пластиной между Pressure carryover angle и радианы (180 степени) друг от друга. Угол поворота диска устанавливается сигналом на порт G. Угол положения цилиндра, γ, является суммой сигнала положения, G и начального смещения угла, Phase angle γ 0 :
γ всегда находится между 0 и 2,. Для любого комбинированного сигнала и смещения больше, чем 2, рад, γ поддерживается на уровне 2, и для любого комбинированного сигнала и смещения ниже, чем 0 рад, и γ поддерживается на уровне 0. Чтобы изменить начальное положение отверстия относительно паза, можно настроить параметр Phase angle.
Аксиально-поршневая машина с пятью поршнями
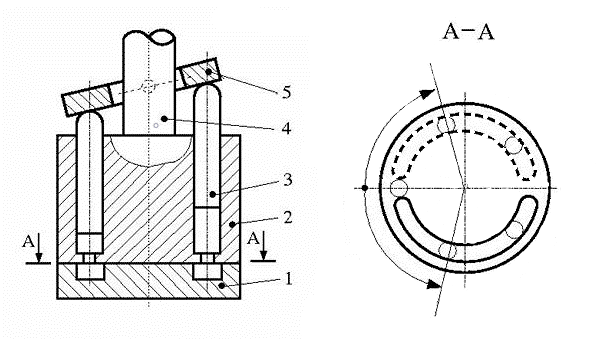
Цифры в схеме указывают компоненты аксиально-поршневой машины:
Отверстие диска клапана
Ротор
Поршень
Ведущий вал
Наклонный диск
Вращательное выравнивание цилиндра с пазом описывается следующими углами:
Угол цилиндра при повороте на паз, γ 1 :
Угол цилиндра при полном повороте на паз, γ 2 :
Угол цилиндра при повороте за паз, γ 3 :
Угол цилиндра при полном повороте за паз, γ 4 :
где:
Ψ является Pressure carryover angle. Этот угол представляет среднее угловое расстояние, на котором поршень перемещается в период перехода давления от закрытого к открытому пазу.
r - половина Cylinder orifice diameter.
R является Cylinder block pitch radius.
Вычисление площади постоянного отверстия во время движения цилиндра
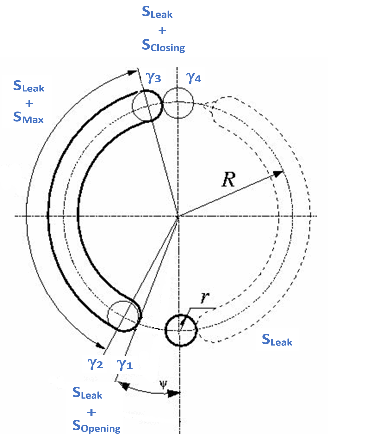
Площадь открытия перехода, которая является открытием между углами поворота цилиндра γ 1 и γ 2, вычисляется как:
Площадь закрытия перехода, которая является открытием между углами поворота цилиндра γ 3 и γ 4, вычисляется как:
где параметры открытия и закрытия:
и
Область между γ 2 и γ 3 и область между γ 4 и γ 1 Максимальное открытие отверстия
Ненулевая Smoothing factor может обеспечить дополнительную числовую стабильность, когда отверстие находится в почти закрытом или почти открытом положении.
На входных и выходных углах паза отверстия можно поддерживать числовую робастность в симуляции, настраивая Smoothing factor блоков. Функция сглаживания применяется ко всем вычисленным углам, но в основном влияет на симуляцию в крайних точках этой области значений.
Нормированный угол открытия перехода вычисляется как:
Smoothing factor, s, применяется к нормированному углу:
Сглаженный угол открытия перехода:
Точно так же нормированный угол закрытия перехода является:
Smoothing factor, s, применяется к нормированному углу:
Сглаженный угол закрытия перехода является:
Поток через отверстие клапана диска вычисляется из зависимости площадь-давления:
где:
C d является Discharge coefficient.
A отверстие является площадью, открытой для потока.
- средняя плотность жидкости.
Δp - перепад давления над клапаном, P A - P B.
Критическое различие давления, Δp крик, является перепадом давления, связанным с Critical Reynolds number, Re криком, который является точкой перехода между ламинарным и турбулентным потоком в жидкости: