Общее сопротивление в двухфазной гидравлической ветви
Simscape/Библиотека фундаментов/Двухфазная жидкость/Элементы
Блок Flow Resistance (2P) моделирует общий перепад давления в двухфазной гидросистеме ветви. Перепад давления пропорционален квадрату массового расхода жидкости и плотности двухфазной жидкости. Константа пропорциональности определяется из номинального рабочего условия, заданного в диалоговом окне блока.
Используйте этот блок, когда единственными данными, доступными для компонента, являются перепад давления в зависимости от его массового расхода жидкости. Объедините блок с другими, чтобы создать собственный компонент, который более точно захватывает перепад давления, который он вызывает - например, теплообменник на основе камерного блока.
Объем жидкости в сопротивлении потоку принят незначительным. Массовый расход жидкости через один порт должен в точности равняться массовому расходу жидкости через другой порт:
где и заданы как массовые расходы жидкости в компонент через порты А и B, соответственно.
Энергия может войти и покинуть сопротивление потоку только через двухфазные порты жидкости. Теплообмен между стенкой и окружением не происходит. В сложение никакая работа не выполняется ни с жидкостью, ни с ней. Энергия, скорость потока жидкости через один порт, должна в точности равняться энергии, скорость потока жидкости через другой порт:
где ϕ A и ϕ B - скорости потока жидкости энергии в сопротивление потоку через порты А и B.
Соответствующие внешние силы на жидкости включают силы, вызванные давлением в портах, и силы вязкого трения на стенках компонента. Гравитация игнорируется, как и другие силы тела. Выражение сил трения в терминах коэффициента потерь ξ приводит к полу-эмпирическому выражению:
где:
Δp - перепад давления от порта А до порта B - то есть p A + p B.
ξ - коэффициент потерь.
ν - удельный объем, обратный плотности массы ρ - то есть 1/ ρ.
S - площадь потока.
Уравнение перепада давления реализовано с двумя модификациями. Во-первых, чтобы разрешить изменение знака при повороте направления потока, оно переписывается:
где перепад давления положителен, только если массовый расход жидкости тоже. Во-вторых, чтобы исключить особенности из-за обращения потока - особенности, которые могут поставить задачу для численных решателей во время симуляции - она линеаризируется в небольшой области почти нулевого потока:
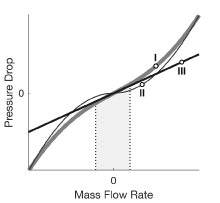
где - порог массовый расход жидкости, ниже которого линеаризируется перепад давления. Рисунок показывает изменение перепада давления относительно локального массового расхода жидкости (кривая I):
Выше , перепад давления аппроксимируется, что выражается в исходном уравнении (кривая II), и оно изменяется с . Эта зависимость соизмерима с зависимостью, наблюдаемой в турбулентных потоках.
Ниже , перепад давления аппроксимирует прямую линию с наклоном, частично зависимым от (кривая III), и она изменяется с . Эта зависимость соизмерима с зависимостью, наблюдаемой в ламинарных течениях.
Для простоты моделирования ξ коэффициента потерь не требуется в качестве параметров блоков. Вместо этого он автоматически вычисляется из номинального условия, заданного в диалоговом окне блока:
где звездочка (*) обозначает значение в номинальном рабочем условии. Основой всех этих вычислений является предположение, что пороговый массовый расход жидкости намного меньше номинального значения . Замена дроби ξ/( 2S2) в выражении для перепада давления дает:
или, эквивалентно:
где C является константой пропорциональности между перепадом давления через сопротивление потоку и локальным массовым расходом жидкости. Он определяется как:
Если определенный объем - и, следовательно, массовая плотность - приняты инвариантными, то его номинальные и фактические значения должны всегда быть равны. Это происходит всякий раз, когда номинальное значение задается в диалоговом окне блока следующим 0- специальное значение, используемое для сигнала блоку, что конкретный объем является константой. Соотношение двух затем 1 и продукт, C ν, уменьшается до: