Номинальные значения обеспечивают способ задать ожидаемую величину переменной в модели, подобный указанию номинала трансформатора или установке области значений на вольтметре. В этом примере показано, как можно точно настроить масштабирование отдельных переменных в модели, чтобы улучшить эффективность решателя и увеличить сходимость моделирования.
Когда решатель выполняет численную симуляцию и анализ, он использует переменные без модулей. Номинальные значения являются способом преобразовать инженерные переменные с модулями измерения в переменные без модулей и масштабировать их для оптимальной эффективности решателя. Номинальное значение имеет значение с модулем, и этот модуль используется для удаления модуля для численных вычислений. Номинальное значение затем определяет величину переменной, как видится численными алгоритмами. Обычно выгодно иметь величины аналогичной шкалы.
Рассмотрим простую модель масса-пружина-демпфер с большого коэффициента упругости.
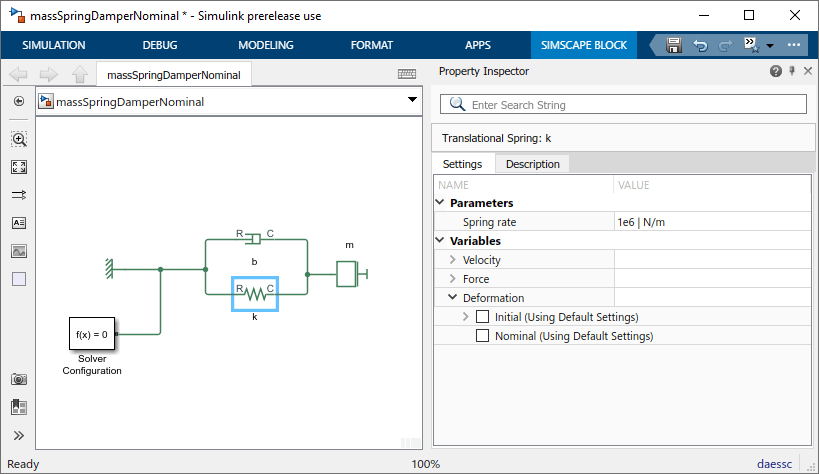
Модель использует настройки параметров блоков по умолчанию, за исключением скорости пружины:
Скорость пружины, k = 1e6 Н/м
Коэффициент демпфирования, b = 100 Н/( м/с)
Масса, m = 1 кг
Начальная переменная массовой скорости, v, имеет High приоритет и начальное целевое значение 0,1 м/с. Модель использует номинальные значения по умолчанию с m как модуль измерения длины.
Когда вы моделируете эту модель, переменная Deformation пружины (положение) x маленькая, в области значений 10 ^ -5 м.

Откройте Solver Profiler, щелкнув гиперссылку в правом нижнем углу окна модели.
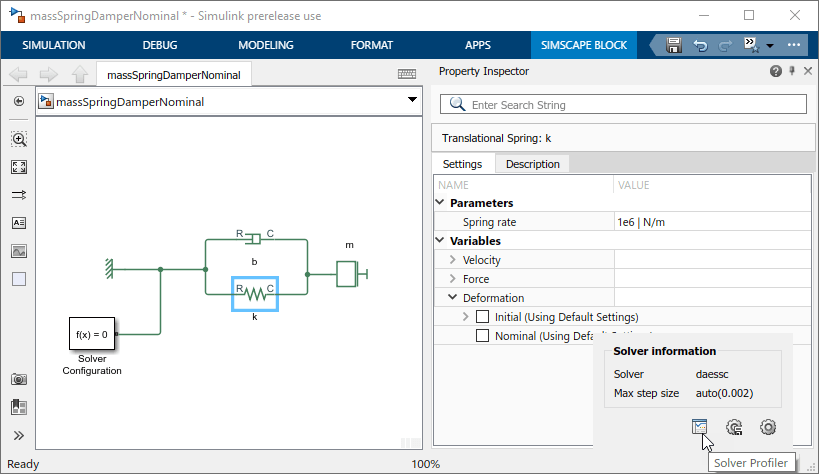
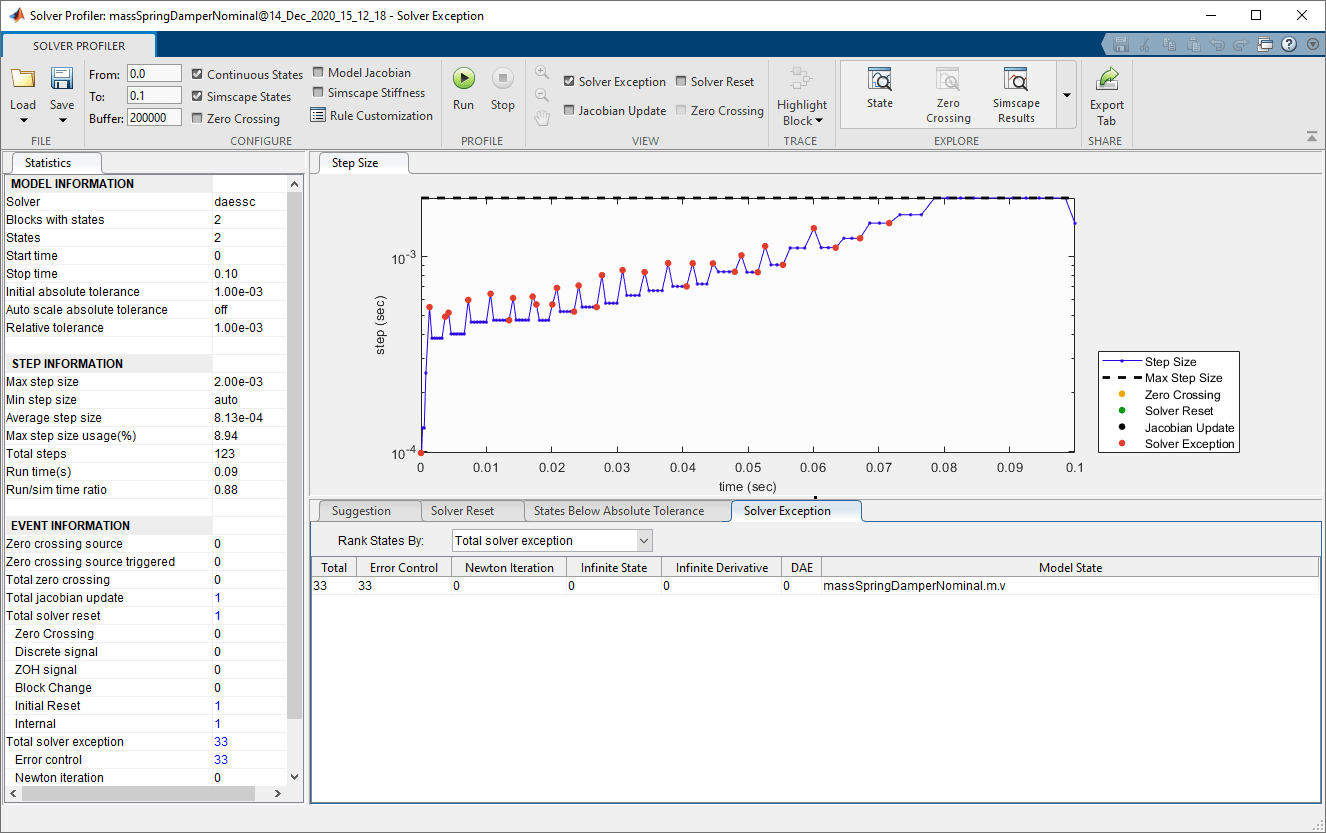
Решатель полностью игнорирует переменную положения и просто смотрит на переменную скорости. Числовая величина положения ниже допуска для этой переменной.
State Viewer, доступный с панели инструментов Solver Profiler, показывает величину каждой переменной, видимую решателями.
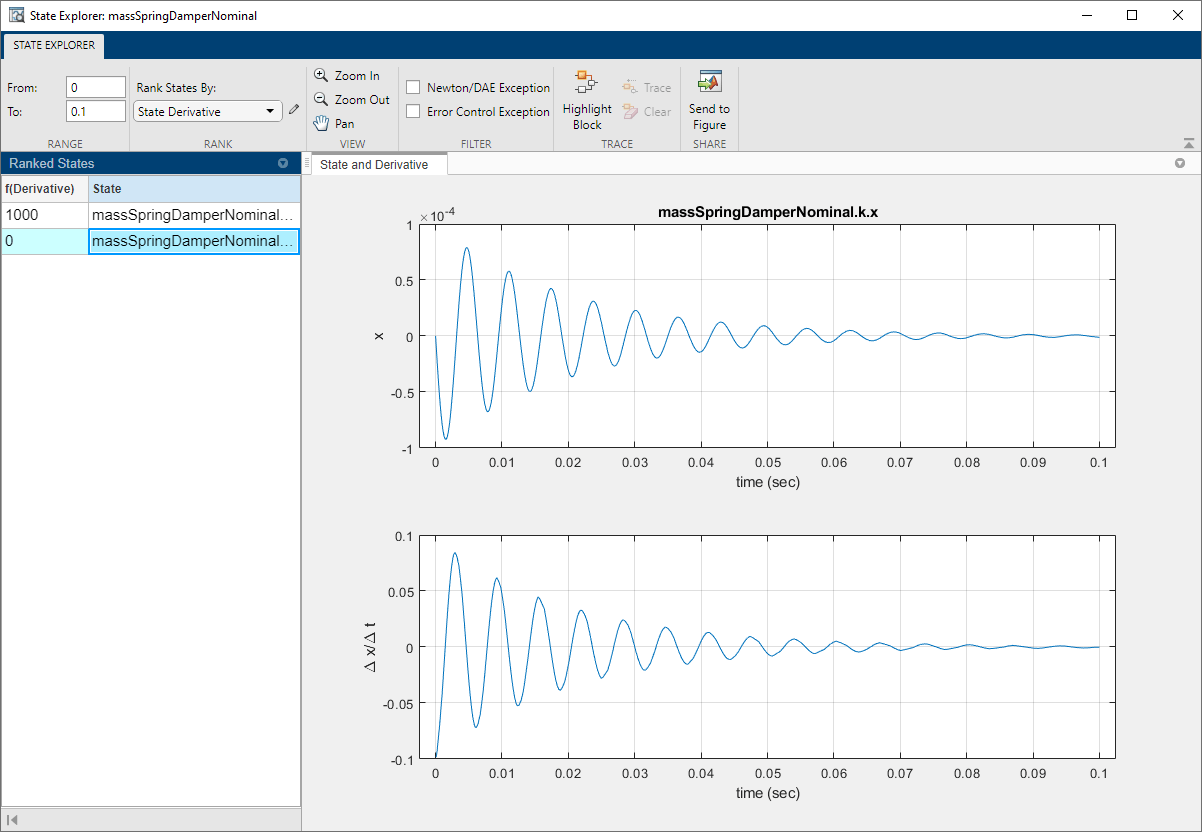
Ситуация ясна, если мы рассмотрим уравнения модели:
Когда k очень большая, по сравнению с m и b, тогда x маленькая, так что произведение k * x имеет разумный размер, по сравнению с другими терминами в уравнении. Чтобы исправить ситуацию, мы должны масштабировать x. Другими словами, нам нужно выбрать номинальное значение для x, которое является маленьким, так что масштабированная переменная, x s, станет более разумным размером:
где c большая. Для примера, если номинальное значение составляет 1 мкм, а исходное x находится в m, то c равно 1e6. Тогда уравнения станут:
и термины имеют величины аналогичной шкалы.
Давайте применим этот принцип масштабирования к переменным модели. Во-первых, используйте Property Inspector, чтобы изменить номинальное значение переменной пружины Deformation x на 100 um (1e-4 м).
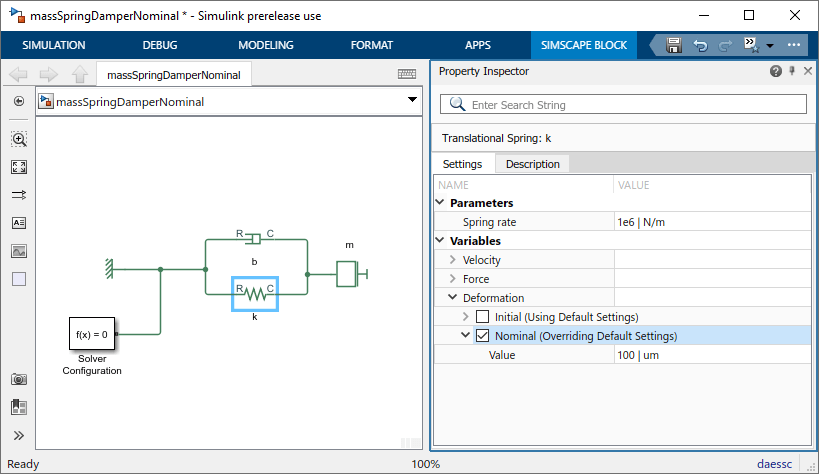
Точно так же измените номинальное значение Velocity массы, переменное, на 10 см/с (0,1 м/с).
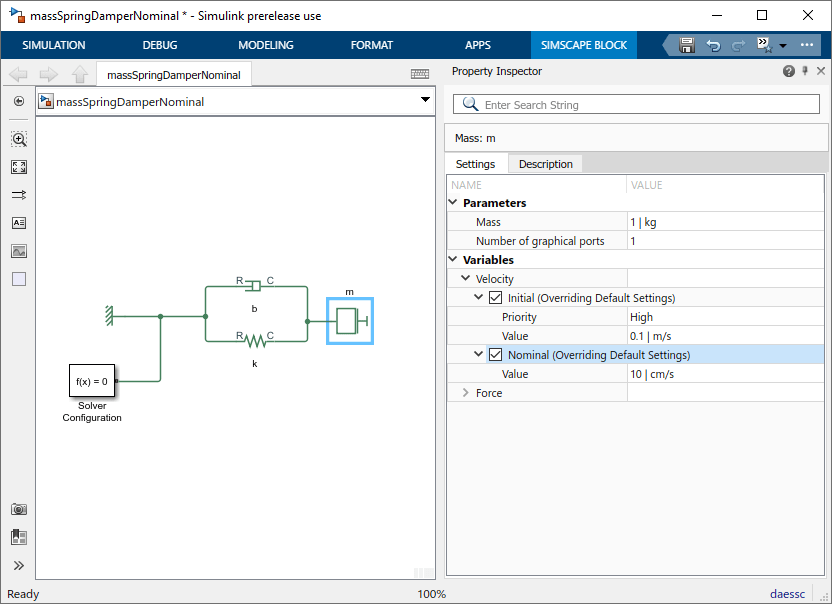
Это приводит шкалу величины обеих переменных, наблюдаемых решателем, к приблизительно 1.
Перезапустите симуляцию.
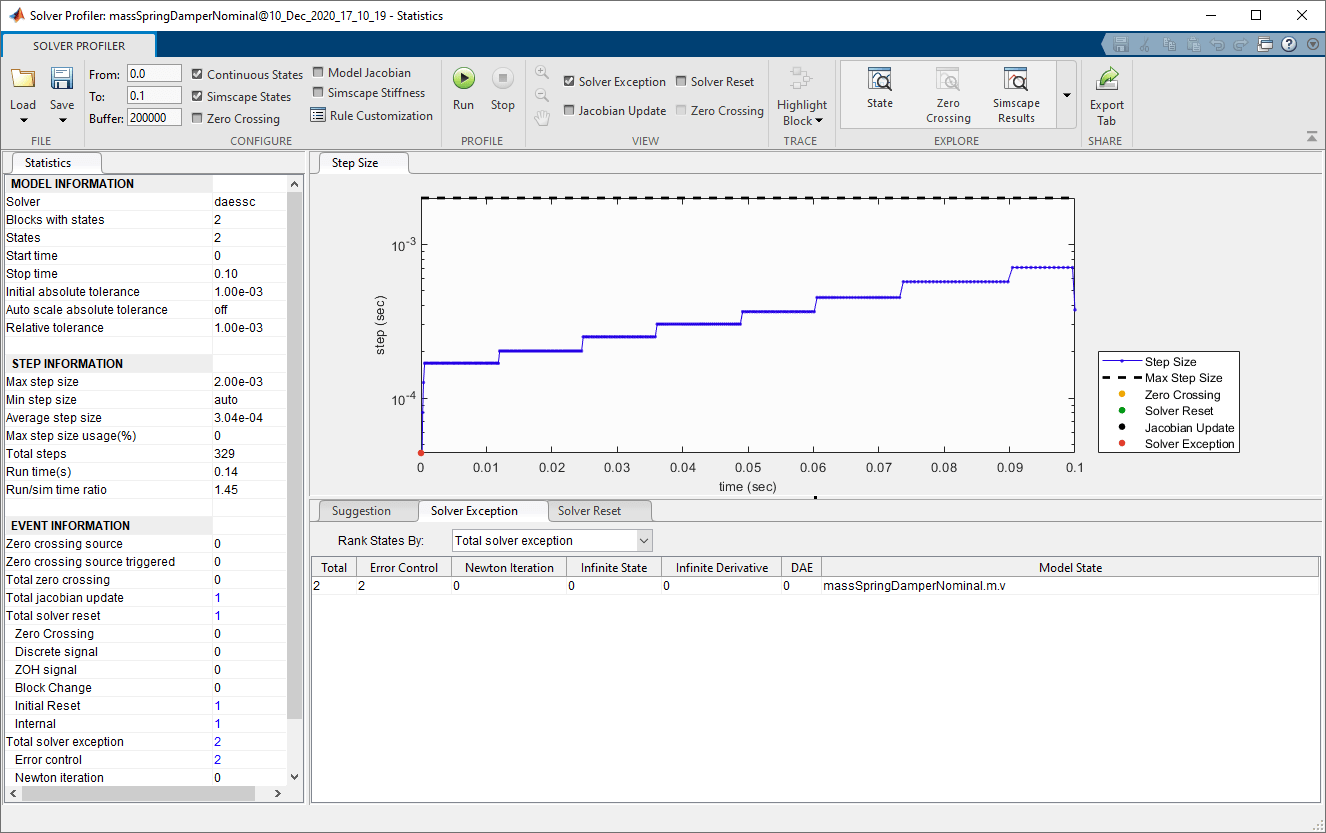
Теперь существует только две исключения решателя, в начале симуляции.
Обратите внимание, что эффективная абсолютная погрешность теперь плотнее для массовой скорости. Эффективная абсолютная погрешность для моделей Simscape™ имеет модуль измерения и вычисляется как (номинальное значение * глобальное AbsTol без модулей). В первом прогоне симуляции эффективная абсолютная погрешность составляла 1e-3 м/с, а теперь он равен 1e-4 м/с, потому что номинальное значение изменило величину и глобальное AbsTol все еще 1e-3. Однако скорость симуляции схожа даже с увеличенной AbsTol о массовой скорости и увеличенных временных шагах.
Значения, как видит решатель, одинаковы по величине как для переменных скорости, так и для переменных положения.
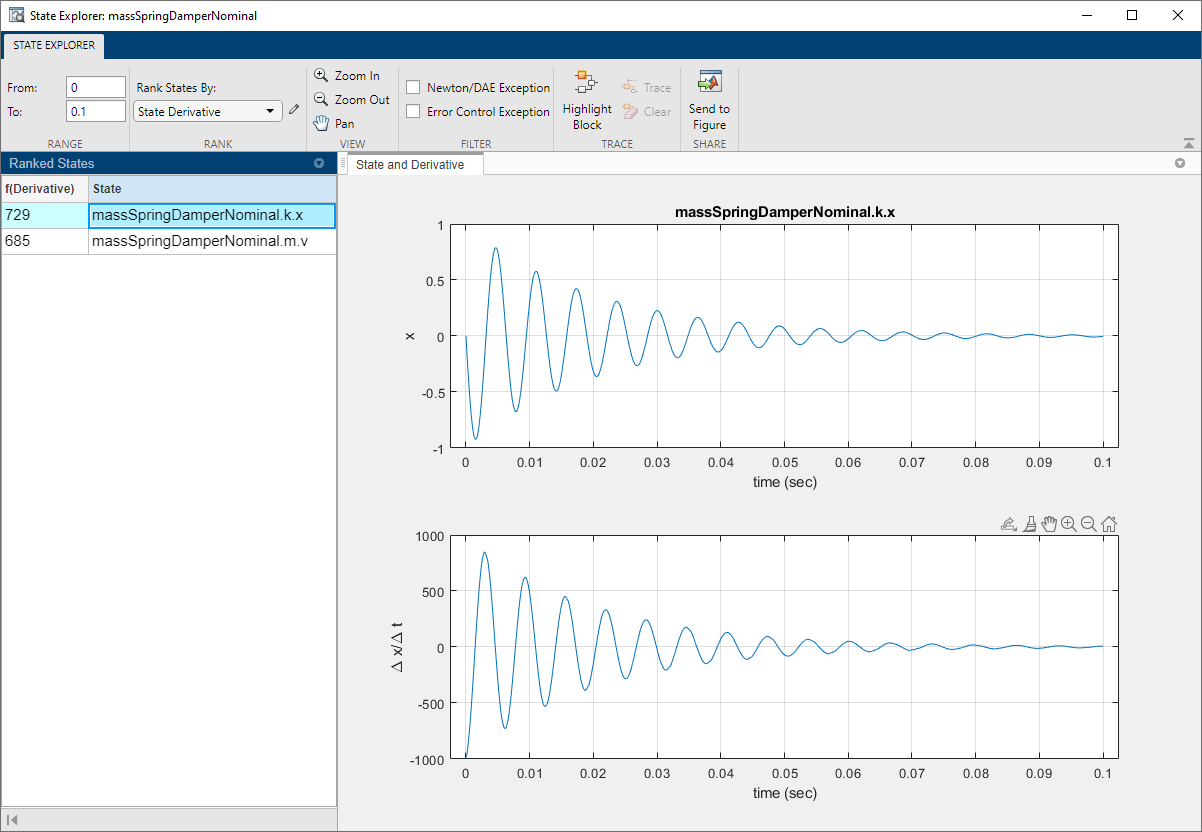
Теперь измените глобальное AbsTol на 1e-2, чтобы более точно соответствовать точности переменной скорости во время первого запуска симуляции.
Перезапустите симуляцию.
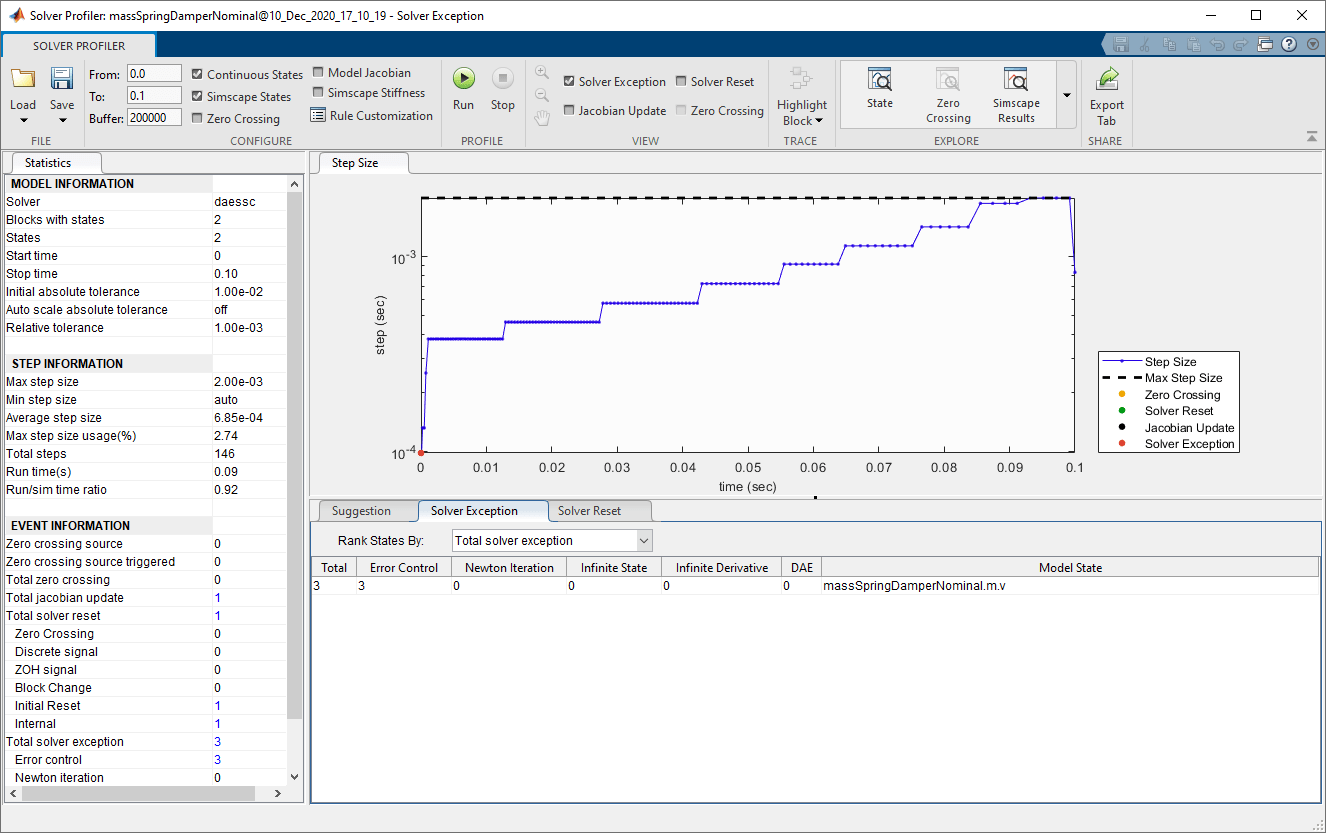
Временные интервалы аналогичны, и количество исключений составляет 3, также в начале симуляции.