abc to dq0, dq0 to abc

Выполните преобразование из трехфазного (abc) сигнала во вращающуюся систему координат dq0 или обратный кадр

Библиотека:
Simscape / Электрический / Специализированные Энергосистемы / Контроль

Описание

Блок abc to dq0 использует преобразование Park, чтобы преобразовать трехфазный (abc) сигнал в вращающуюся систему координат dq0. Угловое положение вращающейся системы координат определяется входом мас., в рад.

Блок dq0 to abc использует обратное преобразование Park, чтобы преобразовать вращающуюся систему координат dq0 в трехфазный (abc) сигнал. Угловое положение вращающейся системы координат определяется входом мас., в рад.

Когда вращающееся выравнивание системы координат при wt = 0 на 90 степени отстает от оси фазы A, сигнал положительной последовательности с Mag = 1 и Фазой = 0 степени приводит к следующим значениям dq: d = 1, q = 0.

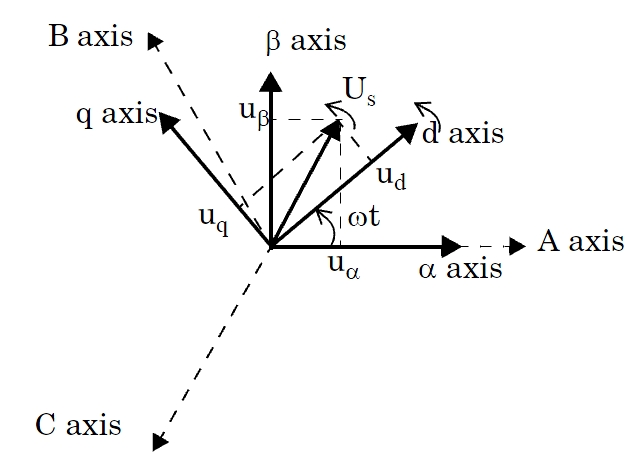
$\begin{matrix} V_{d} = \frac{2}{3} (V_{a} \sin (ω t) + V_{b} \sin (ω t - 2 π / 3) + V_{c} \sin (ω t + 2 π / 3)) \\ V_{q} = \frac{2}{3} (V_{a} \cos (ω t) + V_{b} \cos (ω t - 2 π / 3) + V_{c} \cos (ω t + 2 π / 3)) \\ V_{0} = \frac{1}{3} (V_{a} + V_{b} + V_{c}) \end{matrix}$

$\begin{matrix} V_{a} = V_{d} \sin (ω t) + V_{q} \cos (ω t) + V_{0} \\ V_{b} = V_{d} \sin (ω t - 2 π / 3) + V_{q} \cos (ω t - 2 π / 3) + V_{0} \\ V_{c} = V_{d} \sin (ω t + 2 π / 3) + V_{q} \cos (ω t + 2 π / 3) + V_{0} \end{matrix}$

Блок поддерживает два соглашения, используемые для преобразования Park:

Когда вращающаяся система координат выравнивается по оси A фазы при t = 0, то есть при t = 0, ось d выравнивается по оси a -. Этот тип преобразования Парка также известен как преобразование Парка на основе косинуса.
Когда вращающаяся система координат выровнена на 90 степени позади оси фазы A, то есть при t = 0, ось q выровнена по оси a -. Этот тип преобразования Парка также известен как синусоидальное преобразование Парка. Используйте это преобразование в Simscape™ Electrical™ моделях специализированных степеней с трехфазными синхронными и асинхронными машинами.

Выведите компоненты dq0 из abc-сигналов путем преобразования abc в Богослова в фиксированную опорную систему координат. Затем выполните преобразование α, 0 к dq0 во вращающейся системе координат, то есть выполнив вращение − (и t) на пространстве вектора Us = _uα + j· _uβ.

Преобразование abc-to-dq0 зависит от выравнивания системы координат при t = 0. Положение вращающейся системы координат дано ω.t, где ω представляет скорость вращения системы координат dq.

Когда вращающаяся система координат выровнена по оси A фазы, получаются следующие зависимости:

$\begin{array}{l} U_{s} = u_{d} + j \cdot u_{q} = (u_{a} + j \cdot u_{β}) \cdot e^{- j ω t} = \frac{2}{3} \cdot (u_{a} + u_{b} \cdot e^{\frac{- j 2 π}{3}} + u_{c} \cdot e^{\frac{j 2 π}{3}}) \cdot e^{- j ω t} \\ u_{0} = \frac{1}{3} (u_{a} + u_{b} + u_{c}) \\ [\begin{matrix} u_{d} \\ u_{q} \\ u_{0} \end{matrix}] = \frac{2}{3} [\begin{matrix} \cos (ω t) & \cos (ω t - \frac{2 π}{3}) & \cos (ω t + \frac{2 π}{3}) \\ - \sin (ω t) & - \sin (ω t - \frac{2 π}{3}) & - \sin (ω t + \frac{2 π}{3}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] [\begin{matrix} u_{a} \\ u_{b} \\ u_{c} \end{matrix}] \end{array}$

Обратное преобразование задается:

$[\begin{matrix} u_{a} \\ u_{b} \\ u_{c} \end{matrix}] = [\begin{matrix} \cos (ω t) & - \sin (ω t) & 1 \\ \cos (ω t - \frac{2 π}{3}) & - \sin (ω t - \frac{2 π}{3}) & 1 \\ \cos (ω t + \frac{2 π}{3}) & - \sin (ω t + \frac{2 π}{3}) & 1 \end{matrix}] [\begin{matrix} u_{d} \\ u_{q} \\ u_{0} \end{matrix}]$

Когда вращающаяся система координат выровнена на 90 степени позади оси фазы A, получаются следующие зависимости:

$\begin{array}{l} U_{s} = u_{d} + j \cdot u_{q} = (u_{α} + j \cdot u_{β}) \cdot e^{- j (ω t - \frac{π}{2})} \\ [\begin{matrix} u_{d} \\ u_{q} \\ u_{0} \end{matrix}] = \frac{2}{3} [\begin{matrix} \sin (ω t) & \sin (ω t - \frac{2 π}{3}) & \sin (ω t + \frac{2 π}{3}) \\ \cos (ω t) & \cos (ω t - \frac{2 π}{3}) & \cos (ω t + \frac{2 π}{3}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] [\begin{matrix} u_{a} \\ u_{b} \\ u_{c} \end{matrix}] \end{array}$

Обратное преобразование задается:

$[\begin{matrix} u_{a} \\ u_{b} \\ u_{c} \end{matrix}] = [\begin{matrix} \sin (ω t) & \cos (ω t) & 1 \\ \sin (ω t - \frac{2 π}{3}) & \cos (ω t - \frac{2 π}{3}) & 1 \\ \sin (ω t + \frac{2 π}{3}) & \cos (ω t + \frac{2 π}{3}) & 1 \end{matrix}] [\begin{matrix} u_{d} \\ u_{q} \\ u_{0} \end{matrix}]$

Порты

Вход

расширить все

`abc` - сигнал abc
вектор

abc сигнал, заданный как вектор.

`dq0` - сигнал dq0
вектор

сигнал dq0, заданный как вектор.

`wt` - Угловое положение вращающейся системы координат dq
положительная скалярная величина

Угловое положение вращающейся системы координат dq, в радианах, задается как положительная скалярная величина.

Выход

расширить все

`dq0` - сигнал dq0
вектор

сигнал dq0, возвращенный как вектор.

`abc` - сигнал abc
вектор

abc сигнал, возвращенный как вектор.

Параметры

расширить все

`Rotating frame alignment at wt=0` - Выравнивание вращающейся системы координат
`90 degrees behind phase A axis` (по умолчанию) | `Aligned with phase A axis`

Выравнивание вращающейся системы координат при t = 0 из компонентов dq0 трехфазного сбалансированного сигнала:

$u_{a} = \sin (ω t); u_{b} = \sin (ω t - \frac{2 π}{3}); u_{c} = \sin (ω t + \frac{2 π}{3})$

Величина положительной последовательности равняется 1,0 pu, а угол фазы равен 0 степеням.

Когда вы выбираете Aligned with phase A axisкомпоненты dq0 являются d = 0, q = − 1 и нули = 0.

Когда вы выбираете 90 degrees behind phase A axisкомпоненты dq0 являются d = 1, q = 0 и нули = 0.

Примеры

The power_Transformations пример показывает различные способы использования блоков для выполнения преобразований Кларка и Парка.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

Введенный в R2013a

Документация

abc to dq0, dq0 to abc

Описание

Порты

Вход

`abc` - сигнал abc
вектор

`dq0` - сигнал dq0
вектор

`wt` - Угловое положение вращающейся системы координат dq
положительная скалярная величина

Выход

`dq0` - сигнал dq0
вектор

`abc` - сигнал abc
вектор

Параметры

`Rotating frame alignment at wt=0` - Выравнивание вращающейся системы координат
`90 degrees behind phase A axis` (по умолчанию) | `Aligned with phase A axis`

Примеры

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

Simscape Electrical документация

Поддержка

Документация

abc to dq0, dq0 to abc

Описание

Порты

Вход

abc - сигнал abc вектор

dq0 - сигнал dq0 вектор

wt - Угловое положение вращающейся системы координат dq положительная скалярная величина

Выход

dq0 - сигнал dq0 вектор

abc - сигнал abc вектор

Параметры

Rotating frame alignment at wt=0 - Выравнивание вращающейся системы координат 90 degrees behind phase A axis (по умолчанию) | Aligned with phase A axis

Примеры

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

Simscape Electrical документация

Поддержка

`abc` - сигнал abc
вектор

`dq0` - сигнал dq0
вектор

`wt` - Угловое положение вращающейся системы координат dq
положительная скалярная величина

`dq0` - сигнал dq0
вектор

`abc` - сигнал abc
вектор

`Rotating frame alignment at wt=0` - Выравнивание вращающейся системы координат
`90 degrees behind phase A axis` (по умолчанию) | `Aligned with phase A axis`

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®