Alpha-Beta-Zero to dq0, dq0 to Alpha-Beta-Zero

Выполните преобразование от α, 0 стационарные системы координат до dq0 вращающейся системы координат или обратного

Библиотека

Simscape / Электрический / Специализированные Энергосистемы / Контроль

Описание

Блок Alpha-Beta-Zero to dq0 выполняет преобразование q-0 компонентов Кларка в фиксированной опорной системе координат к d-q0 компонентам Парка во вращающейся опорной системе координат.

Блок dq0 to Alpha-Beta-Zero выполняет преобразование компонентов dq0 Park во вращающейся опорной системе координат к компонентам Бога в фиксированной системе отсчета.

Блок поддерживает два соглашения, используемые в литературе для преобразования Парка:

Вращающаяся система координат, выровненный по оси A при t = 0. Этот тип преобразования Парка также известен как преобразование Парка на основе косинуса.
Вращающаяся система координат выровнена на 90 степени позади оси А. Этот тип преобразования Парка также известен как синусоидальное преобразование Парка. Используйте его в Simscape™ Electrical™ моделях специализированных степеней трехфазных синхронных и асинхронных машин.

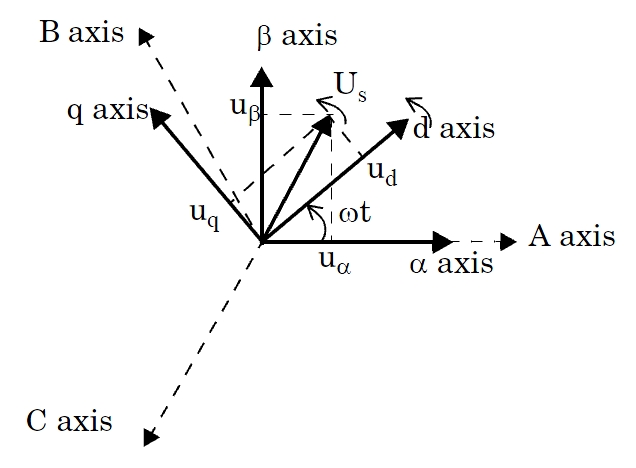
Зная, что положение вращающейся системы координат задано и, что, как показано на фиг.t (где и представляет собой скорость поворота системы координат), преобразование α и dq0 выполняет − вращение на векторе пространства _Us = _uα + j· _uβ. Компонент с гомополярной или нулевой последовательностью остается неизменным.

В зависимости от выравнивания системы координат при t = 0, компоненты dq0 выводятся из компонентов α

Когда вращающаяся система координат выровнена по оси A, получаются следующие зависимости:

$\begin{array}{l} U_{s} = u_{d} + j \cdot u_{q} = (u_{a} + j \cdot u_{β}) \cdot e^{- j ω t} \\ [\begin{matrix} u_{d} \\ u_{q} \\ u_{0} \end{matrix}] = [\begin{matrix} \cos (ω t) & \sin (ω t) & 0 \\ - \sin (ω t) & \cos (ω t) & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} u_{a} \\ u_{β} \\ u_{0} \end{matrix}] \end{array}$

Обратное преобразование задается как

$\begin{array}{l} u_{α} + j \cdot u_{β} = (u_{d} + j \cdot u_{q}) \cdot e^{j ω t} \\ [\begin{matrix} u_{α} \\ u_{β} \\ u_{0} \end{matrix}] = [\begin{matrix} \cos (ω t) & - \sin (ω t) & 0 \\ \sin (ω t) & \cos (ω t) & 0 \\ 0 & 0 & 1 \end{matrix}] [\begin{matrix} u_{d} \\ u q \\ u_{0} \end{matrix}] \end{array}$

Когда вращающаяся система координат выровнена на 90 степени позади оси A, получаются следующие зависимости:

$\begin{array}{l} U_{s} = u_{d} + j \cdot u_{q} = (u_{α} + j \cdot u_{β}) \cdot e^{- j (ω t - \frac{π}{2})} \\ [\begin{matrix} u_{d} \\ u_{q} \\ u_{0} \end{matrix}] = \frac{2}{3} [\begin{matrix} \sin (ω t) & \sin (ω t - \frac{2 π}{3}) & \sin (ω t + \frac{2 π}{3}) \\ \cos (ω t) & \cos (ω t - \frac{2 π}{3}) & \cos (ω t + \frac{2 π}{3}) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{matrix}] [\begin{matrix} u_{a} \\ u_{b} \\ u_{c} \end{matrix}] \end{array}$

Обратное преобразование задается как

$u_{α} + j \cdot u_{β} = (u_{d} + j \cdot u_{q}) \cdot e^{j (ω t - \frac{π}{2})}$

Преобразование abc-to-Alpha-Beta-Zero, примененное к набору сбалансированных трехфазных синусоидальных величин _ua, _ub, _uc, производит пространственный вектор _Us, координаты _uα и _uβ которого в фиксированной исходной системе координат изменяются синусоидально со временем. Напротив, преобразование abc-to-dq0 (преобразование Парка), примененное к набору сбалансированных трехфазных синусоидальных величин _ua, _ub, _uc, создает вектор пространства _Us, координаты _ud и _uq которого в dq вращающейся опорной системе координат остаются постоянными.

Параметры

Rotating frame alignment (at wt=0)

Выберите выравнивание вращающейся системы координат, когда wt = 0, из компонентов dq0 трехфазного сбалансированного сигнала:

$u_{a} = \sin (ω t); u_{b} = \sin (ω t - \frac{2 π}{3}); u_{c} = \sin (ω t + \frac{2 π}{3})$

(амплитуда положительной последовательности = 1,0 pu; угол фазы = 0 степени)

Когда вы выбираете Aligned with phase A axisкомпоненты dq0 являются d = 0, q = − 1 и нули = 0.

Когда вы выбираете 90 degrees behind phase A axis, опция по умолчанию, компоненты dq0 d = 1, q = 0 и нуль = 0.

Входы и выходы

αβ0: Векторизованный сигнал α,
dq0: Векторизованный сигнал dq0.
wt: Угловое положение, в радианах, вращающейся системы координат dq относительно стационарной системы координат.

Пример

The power_Transformations пример показывает различные использования блоков, выполняющих преобразования Кларка и Парка.

Введенный в R2013a

Документация