Когда вы используете фильтр Калмана для отслеживания объектов, вы используете последовательность обнаружений или измерений, чтобы создать модель движения объекта. Движение объекта определяется эволюцией состояния объекта. Фильтр Калмана является оптимальным рекурсивным алгоритмом для оценки дорожки объекта. Фильтр рекурсивен, потому что он обновляет текущее состояние с помощью предыдущего состояния, используя измерения, которые могли быть сделаны в интервале. Фильтр Калмана включает эти новые измерения, чтобы сохранить оценку состояния максимально точной. Фильтр оптимален, потому что он минимизирует среднеквадратическую ошибку состояния. Можно использовать фильтр для предсказания будущих состояний или оценки текущего состояния или прошлого состояния.
Для большинства типов объектов, отслеживаемых в тулбоксе, вектор состояния состоит из одно-, двух- или трехмерных положений и скоростей.
Начните с уравнений Ньютона для объекта, перемещающегося в x -направлении при постоянном ускорении и преобразуйте эти уравнения в форму пространство-состояние.
Если вы задаете состояние как
можно написать закон Ньютона в форме пространства состояний.
Вы используете линейную динамическую модель, когда у вас есть доверие, что объект следует этому типу движения. Иногда модель включает process noise, чтобы отразить неопределенность в модели движения. В этом случае уравнения Ньютона имеют дополнительный член.
vk - неизвестные шумовые возмущения ускорения. Известна только статистика шума. Принято, что это нулевой Гауссов белый шум.
Можно расширить этот тип уравнения до нескольких размерностей. В двух размерностях уравнение имеет вид
Матрица 4 на 4 с правой стороны является state transition model matrix. Для независимых x- и y- движений эта матрица является блочной диагональю.
Когда вы переходите к дискретному времени, вы интегрируете уравнения движения по длине временного интервала. В дискретной форме для интервала расчета T представление состояния становится
Величина xk+1 является состоянием в дискретном временном k+1, и xk является состоянием в более раннем дискретном времени, k. Если вы включаете шум, уравнение становится сложнее, потому что интегрирование шума не является простым.
Уравнение состояния может быть обобщено на
Fk - матрица переходов состояний, а Gk - матрица управления. Матрица управления учитывает любые известные силы, действующие на объект. Даны обе эти матрицы. Последний член представляет шумоподобные случайные возмущения динамической модели. Шум принимается как нулевой Гауссов белый шум.
Системы непрерывного времени с входным шумом описываются линейными стохастическими дифференциальными уравнениями. Системы дискретного времени с входным шумом описаны линейными стохастическими дифференциальными уравнениями. Представление пространства состояний является математической моделью физической системы, где входы, выходы и переменные состояния связаны связанными уравнениями первого порядка.
Measurements то, что вы наблюдаете о своей системе. Измерения зависят от вектора состояния, но не всегда совпадают с вектором состояния. Для образца в радиолокационной системе измерения могут быть сферическими координатами, такими как область значений, азимут и повышение, в то время как вектор состояний является Декартовым положением и скоростью. Для линейного фильтра Калмана измерения всегда являются линейными функциями вектора состояния, исключая сферические координаты. Для использования сферических координат используйте расширенный фильтр Калмана.
Модель измерения принимает, что фактическое измерение в любой момент связано с текущим состоянием
wk представляет шум измерения на текущем временном шаге. Шум измерения также является белым Гауссовым шумом с ковариационной матрицей, Q описывается Qk = E [nknkT].
Без шума динамические уравнения
Аналогичным образом, модель измерения не имеет никакого вклада шума измерения. В каждом образце шум процесса и измерения не известны. Известна только статистика шума.
Можно поместить эти уравнения в рекурсивный цикл, чтобы оценить, как развивается состояние, а также как развиваются неопределенности в компонентах состояния.
Начните с лучшей оценки состояния, x0/0 и ковариации состояния, P0/0. Фильтр выполняет эти шаги в непрерывном цикле.
Распространите состояние на следующий шаг, используя уравнения движения.
Распространите ковариация матрицу.
Обозначение k+1|k индекса указывает, что величина является оптимальной оценкой на k+1 шаге, распространенном из шага k. Эта оценка часто называется априорной оценкой.
Затем спрогнозируйте измерение в обновленное время.
Используйте различие между фактическим и предсказанным измерениями, чтобы исправить состояние в обновленное время. Коррекция требует вычисления усиления Калмана. Для этого сначала вычислите ковариацию предсказания измерения (инновация)
Тогда усиление Калмана
и получают из использования условия оптимальности.
Исправьте предсказанную оценку с помощью измерения. Предположим, что оценка является линейной комбинацией предсказанного состояния и измерения. В оценке после коррекции используется индекс обозначения, k+1|k+1. вычисляется из
где Kk+1 - коэффициент усиления Калмана. Исправленное состояние часто называют апостериорной оценкой состояния, потому что оно выводится после включения измерения.
Исправьте ковариационную матрицу состояний
Наконец, можно вычислить измерение на основе исправленного состояния. Это не коррекция измерения, а лучшая оценка того, что измерение было бы основано на наилучшей оценке состояния. Сравнение этого с фактическим измерением дает вам указание на эффективность фильтра.
Этот рисунок результирующих операций цикла Калмана.
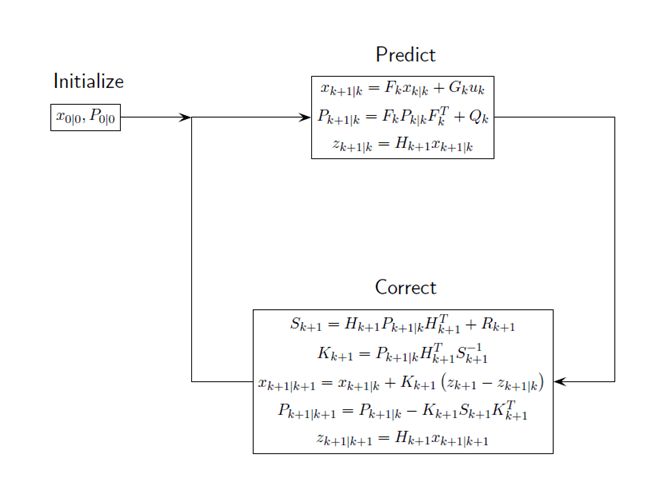
Линейный фильтр Калмана содержит встроенную линейную модель движения с постоянной скоростью. Кроме того, можно задать матрицу перехода для линейного движения. Обновление состояния на следующем временном шаге является линейной функцией состояния в настоящее время. В этом фильтре измерения также являются линейными функциями состояния, описанного матрицей измерений. Для объекта, перемещающегося в трехмерном пространстве, состояние описывается положением и скоростью в x -, y - и z - координатах. Модель перехода состояния для движения с постоянной скоростью
Модель измерения является линейной функцией вектора состояния. Самый простой случай является одним, где измерения являются компонентами положения состояния.
Линейный фильтр Калмана содержит встроенную линейную модель движения с постоянным ускорением. Кроме того, можно задать матрицу перехода для линейного движения с постоянным ускорением. Модель перехода для линейного ускорения
Самый простой случай является одним, где измерения являются компонентами положения состояния.