Для неявных решателей, Simulink® необходимо вычислить решатель Jacobian, который является подматрицей матрицы Якобия, связанной с непрерывным представлением модели Simulink. В целом это непрерывное представление имеет вид:
Якобиан, J, сформирован из этой системы уравнений:
В свою очередь, решатель Якобиан является подматрицей, .
Для многих физических систем решатель Якобиан Jx разрежен, что означает, что многие элементы Jx равны нулю.
Рассмотрим следующую систему уравнений:
Из этой системы можно вывести шаблон разреженности, который отражает структуру уравнений. Шаблон, логическая матрица, имеет 1 для каждой это явным образом появляется в правой части уравнения. Поэтому вы получаете:
Разреженные возмущения и разреженные аналитические методы могут быть способны использовать эту разреженность в шаблон уменьшения количества расчетов, необходимых и улучшения эффективности.
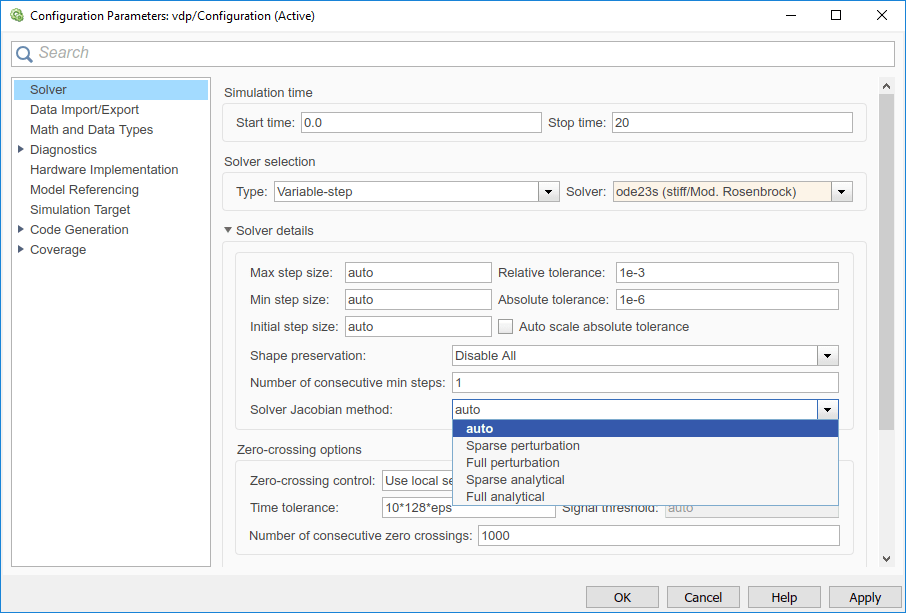
Когда вы выбираете неявный решатель из панели Solver диалогового окна параметров конфигурации, параметр называется Solver Jacobian method появится раскрывающееся меню. В этом меню есть пять опций вычисления решателя Jacobian.
Примечание
Если вы задаете Automatic solver parameter selection error на панели Solver Diagnostics, и вы выбираете другой решатель, чем предложено Simulink, вы можете получить ошибку.
Методы Якобиана решателя имеют эти ограничения, связанные с ними.
Если вы выбираете аналитический якобианский метод, но один или несколько блоков в модели не имеют аналитического якобиана, то Simulink применяет метод возмущения.
Если вы выбираете разреженное возмущение, и ваша модель содержит блоки хранилища данных, Simulink применяет метод полного возмущения.
Настройка по умолчанию для Solver Jacobian method является auto. Выбор этого выбора заставляет Simulink определить, какой из остальных четырех методов лучше всего подходит вашей модели. Эта блок-схема изображает алгоритм.
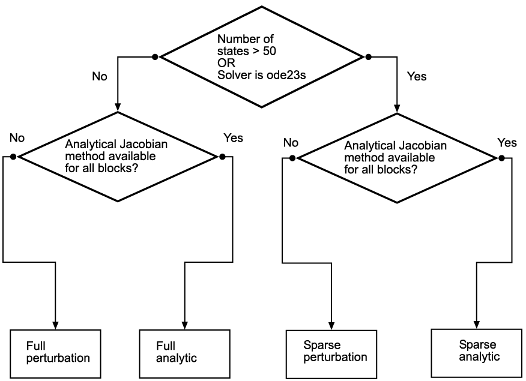
Разреженные методы выгодны для моделей, которые имеют большое количество состояний. Если в вашей модели существует 50 или более состояний, auto выбирает разреженный метод. В отличие от других неявных решателей, ode23s является разреженным методом, потому что он генерирует новый якобиан на каждом временном шаге. Поэтому выгоден разреженный аналитический или разреженный метод возмущения. Выбор auto также гарантирует, что аналитические методы используются только, если каждый блок в вашей модели может сгенерировать аналитический якобиан.
Метод полного возмущения решает полный набор уравнений возмущения и использует LAPACK для линейных алгебраических операций. Этот метод является дорогостоящим с вычислительной точки зрения, но остается рекомендуемым методом для установления базовых результатов.
Разреженный метод возмущения пытается улучшить эффективность во время выполнения, используя математическое преимущество разреженного якобианского шаблона. Возвращаясь к системе выборки из трех уравнений и трех состояний,
Решатель Jacobian является:
|
Поэтому необходимо трижды возмущать каждое из трех состояний и трижды вычислять производную функцию. Для системы с n состояниями этот метод n раз возмущает состояния.
Путем применения шаблона разреженности и возмущающих состояний x 1 и x 2 вместе, эта матрица уменьшается до:
|
Теперь решатель может решить столбцы 1 и 2 в одном сдвиге. Хотя разреженный метод возмущения сохраняет значительные расчеты, он также добавляет накладные расходы к компиляции. Это может даже замедлить симуляцию, если система не имеет большого количества непрерывных состояний. Существует переломная точка, для которого вы получаете повышенную эффективность с помощью этого метода. В целом системы, имеющие большое количество непрерывных состояний, обычно разрежены и извлекают выгоду из разреженного метода.
Разреженный метод возмущения, как и разреженный аналитический метод, использует UMFPACK для выполнения линейных алгебраических операций. Кроме того, разреженный метод возмущения поддерживает и RSim, и быстрый режим Accelerator.
Полные и разреженные аналитические методы пытаются улучшить эффективность путем вычисления якобиана с помощью аналитических уравнений, а не уравнений возмущения. Разреженный аналитический метод, также использует информацию разреженности, чтобы ускорить линейные алгебраические операции, необходимые для решения обыкновенных дифференциальных уравнений.
Для получения дополнительной информации о том, как получить доступ и интерпретировать шаблон разреженности в MATLAB®, см. Исследование якобианской структуры решателя модели.
В то время как разреженный метод возмущения поддерживает RSim, разреженный аналитический метод не делает. Следовательно, независимо от того, какой разреженный метод вы выбираете, любой сгенерированный код использует разреженный метод возмущения. Это ограничение распространяется и на быстрые режимы Accelerator.