Марковские процессы являются примерами стохастических процессов - процессов, которые генерируют случайные последовательности результатов или states по определенным вероятностям. Марковские процессы отличаются незабываемостью - их следующее состояние зависит только от их текущего состояния, а не от той истории, которая привела их туда. Модели марковских процессов используются в самых разных приложениях, от ежедневных биржевых цен до позиций генов в хромосоме.
Марковской модели придается визуальное представление со диаграммой состояний, такой как приведенная ниже.
Диаграмма состояний для марковской модели
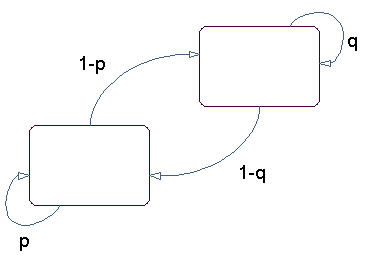
Прямоугольники в схеме представляют возможные состояния процесса, который вы пытаетесь смоделировать, а стрелы представляют переходы между состояниями. Метка на каждой стреле представляет вероятность этого перехода. На каждом шаге процесса модель может сгенерировать выход, или emission, в зависимости от того, в каком состоянии она находится, и затем выполнить переход в другое состояние. Важной характеристикой марковских моделей является то, что следующее состояние зависит только от текущего состояния, а не от истории переходов, которые приводят к текущему состоянию.
Для примера для последовательности монет два состояния являются головами и хвостами. Самый последний подсчет монеты определяет текущее состояние модели, и каждый последующий подсчет определяет переход к следующему состоянию. Если монета справедлива, все вероятности перехода равны 1/2. Выбросы могут быть просто текущим состоянием. В более сложных моделях случайные процессы в каждом состоянии будут генерировать выбросы. Можно, например, прокатать матрицу, чтобы определить выброс на любом шаге.
Markov chains являются математическими описаниями марковских моделей с дискретным набором состояний. Марковские цепи характеризуются:
Набор состояний {1, 2,..., M}
M-на-M transition matrix T, чей i, j вход является вероятностью перехода от i состояния к j состояния. Сумма значений в каждой строке T должна быть 1, потому что это сумма вероятностей перехода от заданного состояния к каждому из других состояний.
Набор возможных выходов или выбросов {s1, s2,..., s N}. По умолчанию набор выбросов {1, 2,..., N}, где N - количество возможных выбросов, но можно выбрать другое значение чисел или символов.
M-на-N emission matrix E, чей i, k вход дает вероятность излучения символа sk, учитывая, что модель находится в i состоянии.
Цепи Маркова начинаются в initial state i 0 на шаге 0. Цепь затем переходит в состояние i1 с вероятностью , и излучает выход с вероятностью . Следовательно, вероятность наблюдения последовательности состояний и последовательность выбросов на первом шаге,