Документация

Введение в частичные наименьшие квадраты

Partial least-squares (PLS) регрессия является методом, используемым с данными, которые содержат коррелированные переменные предиктора. Этот метод создает новые переменные предиктора, известные как components, как линейные комбинации исходных переменных предиктора. PLS строит эти компоненты с учетом наблюдаемых значений отклика, приводя к скупой модели с надежной прогностической степенью.

Метод представляет собой нечто среднее между многофакторной линейной регрессией и анализом основных компонентов:

Поэтому PLS объединяет информацию о отклонениях как предикторов, так и ответов, принимая во внимание также корреляции среди них.

PLS разделяет характеристики с другими методами регрессии и преобразования функций. Он похож на регрессию хребта в том, что используется в ситуациях с коррелированными предикторами. Он похож на ступенчатую регрессию (или более общие методы выбора признаков) тем, что он может использоваться, чтобы выбрать меньший набор членов модели. PLS отличается от этих методов, однако, преобразованием исходного пространства предикторов в новое пространство компонентов.

Функция plsregress выполняет регрессию PLS.

Частичные наименьшие квадраты

Например, рассмотрим данные о биохимической потребности в кислороде в moore.mat, дополненный шумными версиями предикторов для введения корреляций:

load moore
y = moore(:,6);              % Response
X0 = moore(:,1:5);           % Original predictors
X1 = X0+10*randn(size(X0));  % Correlated predictors
X = [X0,X1];

Использовать plsregress чтобы выполнить регрессию PLS с таким же количеством компонентов, что и предикторы, затем постройте график процентного отклонения, объясняемой в отклике, как функция от количества компонентов:

[XL,yl,XS,YS,beta,PCTVAR] = plsregress(X,y,10);

plot(1:10,cumsum(100*PCTVAR(2,:)),'-bo');
xlabel('Number of PLS components');
ylabel('Percent Variance Explained in y');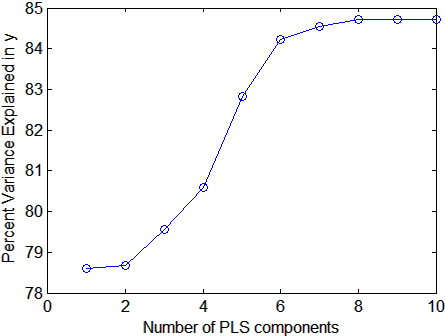

Выбор количества компонентов в модели PLS является критическим шагом. График дает грубое указание, показывая почти 80% отклонения в y объясняется первым компонентом с пятью дополнительными компонентами, вносящими значительный вклад.

Следующая модель вычисляет модель с шестью компонентами:

[XL,yl,XS,YS,beta,PCTVAR,MSE,stats] = plsregress(X,y,6);
yfit = [ones(size(X,1),1) X]*beta;

plot(y,yfit,'o')

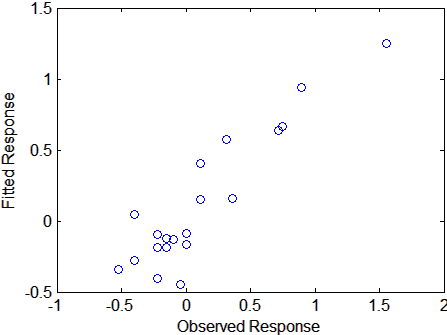
Рассеяние показывает разумную корреляцию между подобранными и наблюдаемыми реакциями, и это подтверждается R² статистический:

TSS = sum((y-mean(y)).^2);
RSS = sum((y-yfit).^2);
Rsquared = 1 - RSS/TSS
Rsquared =
    0.8421

График весов десяти предикторов в каждом из шести компонентов показывает, что два из компонентов (последние два вычисленных) объясняют большую часть отклонения в X:

plot(1:10,stats.W,'o-');
legend({'c1','c2','c3','c4','c5','c6'},'Location','NW')
xlabel('Predictor');
ylabel('Weight');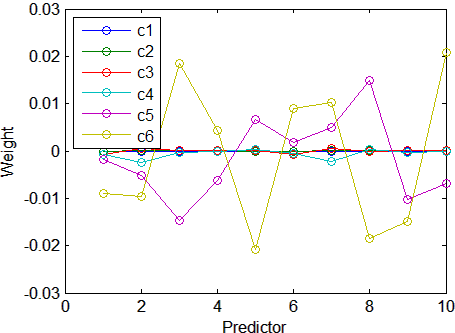

График среднеквадратичных ошибок предполагает, что всего два компонента могут предоставить адекватную модель:

[axes,h1,h2] = plotyy(0:6,MSE(1,:),0:6,MSE(2,:));
set(h1,'Marker','o')
set(h2,'Marker','o')
legend('MSE Predictors','MSE Response')
xlabel('Number of Components')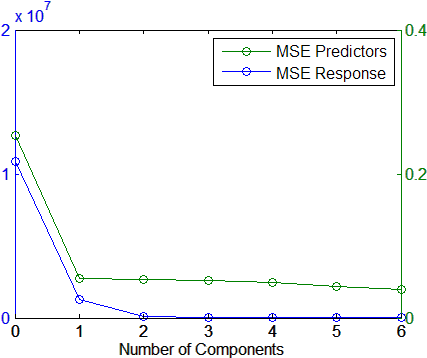

Вычисление среднеквадратичных ошибок plsregress управляется необязательными парами имя/значение параметра, задающими тип перекрестной валидации и количество повторений Монте-Карло.