Фазовая подстройка частоты
Фазовая подстройка частоты комбинирует управляемый напряжением генератор и компаратор фазы как система с обратной связью, чтобы настроить частоту генератора или фазу, чтобы отследить прикладной модулируемый частотой или модулируемый фазой сигнал.
Блоки управляемого напряжением генератора
Управляемый напряжением генератор является одной частью фазовой подстройки частоты. Continuous-Time VCO и Discrete-Time VCO блокируют управляемые напряжением генераторы реализации. Эти блоки производят выходные сигналы непрерывного времени и дискретного времени, соответственно. Выходной сигнал каждого блока является синусоидальным, и изменяет свою частоту в ответ на амплитудные изменения входного сигнала.
Обзор симуляции PLL
Фазовая подстройка частоты (PLL), когда используется в сочетании с другими компонентами, помогает синхронизировать приемник. PLL является автоматической системой управления, которая настраивает фазу локального сигнала совпадать с фазой полученного сигнала. Дизайнерские работы PLL лучше всего для узкополосных сигналов.
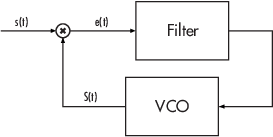
Простой PLL состоит из детектора фазы, контурного фильтра и управляемого напряжением генератора (VCO). Например, следующий рисунок показывает, как эти компоненты располагаются для аналогового PLL полосы пропускания. В этом случае детектор фазы является только множителем. Сигнал e (t) часто называется сигналом ошибки.
Эта таблица показывает поддерживаемые типы PLLs и блоков, которые реализуют их.
Поддерживаемый PLLs в библиотеке компонентов
| Тип PLL | Блок |
|---|---|
| Аналоговый PLL полосы пропускания | Phase-Locked Loop |
| Аналоговый основополосный PLL | Baseband PLL |
| Линеаризовавший аналоговый основополосный PLL | Linearized Baseband PLL |
| Цифровой PLL с помощью насоса заряда | Charge Pump PLL |
Различные PLLs используют различные детекторы фазы, фильтры и характеристики VCO. Некоторые из этих атрибутов встроены в блоки PLL в этом продукте, в то время как другие зависят от параметров, которые вы устанавливаете в маске блока:
Вы задаете передаточную функцию фильтра в маске блока с помощью параметров Lowpass filter denominator и Lowpass filter numerator. Каждый из этих параметров является вектором, который перечисляет коэффициенты соответствующего полинома в порядке убывающих экспонент переменной s. Чтобы спроектировать фильтр, можно использовать функции такой как
butter,cheby1, иcheby2в Signal Processing Toolbox.Вы задаете характеристики ключа VCO в маске блока. Все четыре блока PLL используют параметр VCO input sensitivity. Некоторые блоки также используют VCO quiescent frequency, VCO initial phase и параметры VCO output amplitude.
Детектор фазы для каждого из блоков PLL является функцией, которую вы не можете изменить от маски блока.
Реализация аналогового основополосного PLL
В отличие от моделей полосы пропускания для фазовой подстройки частоты, основополосная модель не зависит от несущей частоты. Это позволяет вам использовать более низкую частоту дискретизации в симуляции. Два блока реализуют аналоговый основополосный PLLs:
Линеаризовавшая модель и не линеаризовавшая модель отличаются по этому, линеаризовавшая модель использует приближение
упростить расчеты. Это приближение близко, когда Δθ (t) является близким нулем. Таким образом, вместо того, чтобы использовать входной сигнал и выходной сигнал VCO непосредственно, линеаризовавшая модель PLL использует только их фазы.
Реализация цифрового PLL
PLL насоса заряда является классическим цифровым PLL. В отличие от аналогового упомянутого выше PLLs, PLL насоса заряда использует детектор фазы последовательной логики, который также известен как цифровой детектор фазы или детектор фазы/частоты.
Выбранная библиография для синхронизации
[1] Гарднер, F.M., “Циклы Charge-pump Phase-lock”, Сделка IEEE на Коммуникациях, Издании 28, ноябрь 1980, стр 1849–1858.
[2] Гарднер, F.M., “Точность фазы Насоса Заряда PLLs”, Сделка IEEE на Коммуникациях, Издании 30, октябрь 1982, стр 2362–2363.
[3] Гупта, Южная Каролина, “Фазовая подстройка частоты”, Продолжения IEEE, Издания 63, февраль 1975, стр 291–306.
[4] Линдси, В.К. и К.М. Чи, “Обзор Цифровой Фазовой подстройки частоты”, Продолжения IEEE, Издания 69, апрель 1981, стр 410–431.
[5] Mengali, Умберто, и Альдо Н. Д'Андреа, методы синхронизации для Диджитэл-Ресиврс, Нью-Йорк, нажатия пленума, 1997.
[6] Meyr, Генрих, и Герд Ашайд, синхронизация в цифровой связи, издании 1, Нью-Йорк, John Wiley & Sons, 1990.
[7] Moeneclaey, Марк и Герт де Жонгх, “Ориентированный на ML на Синхронизацию Несущей NDA для Общих Вращательно Симметричных Сигнальных созвездий”, Транзакции IEEE на Коммуникациях, Издании 42, № 8, август 1994, стр 2531–2533.
[8] Рис, Майкл. Цифровая связь: подход дискретного времени. Верхний Сэддл-Ривер, NJ: Prentice Hall, 2009.