Проколотое сверточное кодирование

Эта модель показывает, как использовать Convolutional Encoder и блоки Viterbi Decoder, чтобы симулировать проколотую систему кодирования. Сложность Декодера Витерби увеличивается быстро со скоростью кода. Прокалывание является методом, который позволяет кодирование и декодирование более высоких кодов уровня с помощью стандартного уровня 1/2 энкодеры и декодеры.

Пример несколько похож на тот, который появляется в Декодировании Мягкого Решения, которое показывает сверточное кодирование без прокалывания.

Структура примера

Этот пример содержит эти блоки.

Bernoulli Binary Generator: Создайте последовательность случайных битов, чтобы использовать в качестве сообщения.
Convolutional Encoder: Закодируйте сообщение с помощью сверточного энкодера.
BPSK Modulator Baseband: Модулируйте закодированное сообщение.
AWGN Channel: Передайте модулируемый сигнал через шумный канал.
Error Rate Calculation: Вычислите количество несоответствий между исходными и восстановленными сообщениями.

Откройте пример, doc_punct_conv_code, путем ввода следующего в MATLAB^® командная строка.

doc_punct_conv_code

Генерация случайных данных

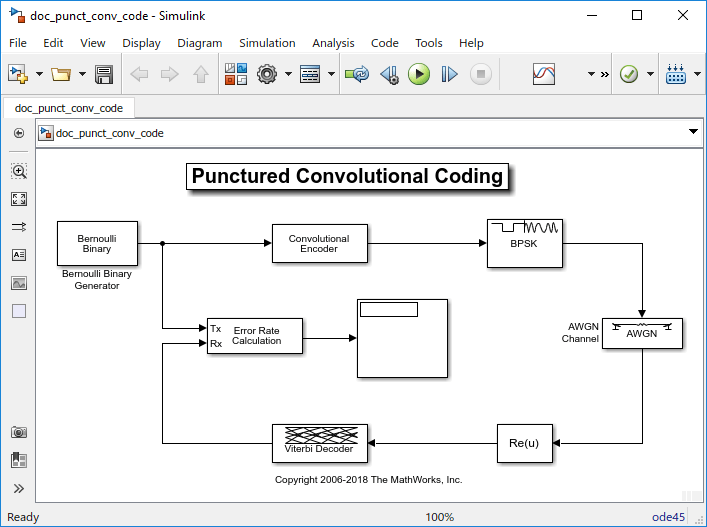
Блок Bernoulli Binary Generator производит источник информации для этой симуляции. Блок генерирует систему координат трех случайных битов в каждом шаге расчета. Параметр Samples per frame определяет количество строк выходной системы координат.

Сверточное кодирование с прокалыванием

Блок Convolutional Encoder кодирует данные из Bernoulli Binary Generator. Этот пример использует тот же код как описано в Декодировании Мягкого Решения.

Шаблон прокола задан параметром Puncture vector в маске. Вектор прокола является вектором столбца двоичных данных. 1 указывает, что бит в соответствующем положении входного вектора отправляется в выходной вектор, в то время как 0 указывает, что бит удален.

Например, чтобы создать уровень 3/4 код от уровня 1/2, продолжительность ограничения 7 сверточных кодов, оптимальный вектор прокола [1 1 0 1 1 0]'. (где'. после того, как вектор указывает на транспонирование). Биты в положениях 1, 2, 4, и 5 передаются, в то время как биты в положениях 3 и 6 удалены. Теперь для каждых 3 битов входа, проколотый код генерирует 4 бита выхода (в противоположность 6 битам, произведенным прежде, чем проколоть). Это делает уровень 3/4.

В этом примере выход от Bernoulli Binary Generator является вектор-столбцом длины 3. Поскольку уровень 1/2 Convolutional Encoder удваивает длину каждого вектора, длина вектора прокола должна разделиться 6.

Передача данных

Блок AWGN Channel симулирует передачу по шумному каналу. Параметры для блока устанавливаются в маске можно следующим образом:

Параметр Mode для этого блока устанавливается на Signal to noise ratio (Es/No).
Параметр Es/No устанавливается на 2 дБ. Это значение обычно изменяется от одной симуляции, запущенной к следующему.
Предыдущий блок модуляции генерирует модульные сигналы степени, таким образом, Input signal power установлен в 1 ватт.
Symbol period установлен в 0,75 секунды, потому что код имеет уровень 3/4.

Демодуляция

В этой симуляции блок Viterbi Decoder собирается принять неквантованные входные параметры. В результате симуляция передает канал выход через Simulink^® Блок Complex to Real-Imag, который извлекает действительную часть комплексных выборок.

Декодирование Viterbi проколотых кодов

Блок Viterbi Decoder сконфигурирован, чтобы декодировать тот же уровень 1/2 код, заданный в блоке Convolutional Encoder.

В этом примере тип решения установлен в Unquantized. Для кодов без прокалывания вы обычно устанавливали бы Traceback depth для этого кода к значению близко к 40. Однако для декодирования проколотых кодов, более высокое значение требуется, чтобы давать декодеру достаточно данных, чтобы разрешить неоднозначности, введенные проколами.

Поскольку проколотые биты не передаются, нет никакой информации, чтобы указать на их значения. В результате они проигнорированы в процессе декодирования.

Параметр Puncture vector указывает на местоположения проколов или битов, чтобы проигнорировать в процессе декодирования. Каждый 1 в векторе прокола указывает на переданный бит, в то время как каждый 0 указывает на прокол или бит, чтобы проигнорировать во входе к декодеру.

В общем случае два параметра Puncture vector в Convolutional Encoder и Viterbi Decoder должны быть тем же самым.

Вычисление коэффициента ошибок

Блок Error Rate Calculation сравнивает декодируемые биты с битами первоисточника. Выход блока Error Rate Calculation является трехэлементным вектором, содержащим расчетную частоту ошибок по битам (BER), количество ошибок, наблюдаемых и количество обработанных битов.

В маске для этого блока параметр Receive delay устанавливается на 96, потому что значение Traceback depth 96 в блоке Viterbi Decoder создает задержку 96. Если бы были другие блоки в модели, которая создала задержки, Receive delay равнялся бы сумме всех задержек.

Произошли симуляции BER, обычно запущенные до минимального количества ошибок, или пока симуляция не обрабатывает максимальное количество битов. Блок Error Rate Calculation использует свой режим Stop simulation, чтобы установить эти пределы и управлять длительностью симуляции.

Оценка результатов

Генерация небольшой кривой коэффициента ошибок требует нескольких симуляций. Можно выполнить несколько симуляций с помощью sim команда. Выполните эти шаги:

В окне модели удалите блок Display и подключенное параллельно к его порту.
В блоке AWGN Channel, установленном параметр Es/No на имя переменной EsNodB.
В блоке Error Rate Calculation, набор Output data к Workspace и затем набор Variable name к BER_Data.
Сохраните модель в своей рабочей директории под другим именем, таким как my_punct_conv_code.slx.

Выполните следующий код, который запускает симуляцию многократно и собирает результаты.

CodeRate = 0.75;
EbNoVec = [2:.5:5];
EsNoVec = EbNoVec + 10*log10(CodeRate);
BERVec = zeros(length(EsNoVec),3);
for n=1:length(EsNoVec),
    EsNodB = EsNoVec(n);
    sim('my_commpunctcnvcod');
    BERVec(n,:) = BER_Data;
end

Чтобы подтвердить валидность результатов, сравните их с установленной связанной эффективностью. Эффективность частоты ошибок по битам уровня r = (n-1)/n проколотый код ограничена выше выражением:

$P_{b} \leq \frac{1}{2 (n - 1)} \sum_{d = d_{f r e e}}^{\infty} ω_{d} erfc (\sqrt{rd (E_{b} {/N}_{0})})$

В этом выражении, erfc обозначает дополнительную функцию ошибок, r является скоростью кода, и и _dfree и _ωd зависят от конкретного кода. Для уровня 3/4 код этого примера, _dfree = 5, _ω5 = 42, _ω6 = 201, _ω7 = 1492, и так далее. Смотрите ссылку [1] для получения дополнительной информации.

Следующие команды вычисляют приближение связанное использование первых семи терминов суммирования (значения, используемые для nerr найдены в Таблице 2 ссылки [2]:

dist = [5:11];
nerr = [42 201 1492 10469 62935 379644 2253373];
CodeRate = 3/4;
EbNo_dB = [2:.02:5];
EbNo = 10.0.^(EbNo_dB/10);
arg = sqrt(CodeRate*EbNo'*dist);
bound = nerr*(1/6)*erfc(arg)';

Чтобы построить симуляцию и теоретические результаты на том же рисунке, используйте команды ниже.

berfit(EbNoVec',BERVec(:,1)); % Curve-fitted simulation results
hold on;
semilogy(EbNo_dB,bound,'g'); % Theoretical results
legend('Simulated BER','Fit for simulated BER',...
    'Theoretical bound on BER')

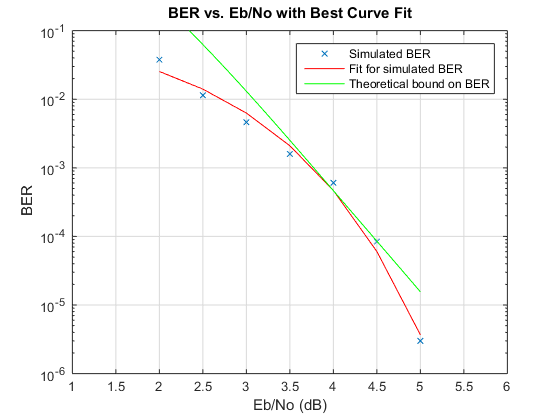
В некоторых случаях, с более низкими частотами ошибок по битам, вы можете заметить результаты симуляции, которые, кажется, указывают на коэффициенты ошибок немного выше связанного. Это может следовать из отклонения симуляции (если меньше чем 500 битовых ошибок наблюдаются), или от конечной traceback глубины в декодере.

Ссылки

[1] Yasuda, Y., К. Кэшики и И. Хирэта, "Высокий показатель Проколотые Сверточные коды для Мягкого Решения Декодирование Viterbi", Транзакции IEEE на Коммуникациях, Издании COM-32, март 1984, стр 315-319.

[2] Начните, G., Haccoun, D. и Пакуин, C., "Дальнейшие результаты на Высоком показателе Проколотые Сверточные коды для Viterbi и Sequential Decoding", Транзакции IEEE на Коммуникациях, Издании 38, № 11, ноябрь 1990, p. 1923.

Документация