ПИД-регуляторы с двумя степенями свободы

Две степени свободы (2-DOF) ПИД-регуляторы включают взвешивание заданного значения на пропорциональных и производных терминах. ПИД-регулятор с 2 степенями свободы способен к быстрому подавлению помех без значительного увеличения перерегулирования в отслеживании заданного значения. ПИД-регуляторы 2-DOF также полезны, чтобы смягчить влияние изменений в опорном сигнале на управляющем сигнале.

Можно представлять ПИД-регуляторы с помощью специализированных объектов модели pid2 и pidstd2. Эта тема описывает представление ПИД-регуляторов 2-DOF в MATLAB^®. Для получения информации об автоматической настройке ПИД-регулятора смотрите, что ПИД-регулятор Настраивается.

Непрерывное время представления ПИД-регулятора 2-DOF

Этот рисунок показывает типичную архитектуру управления с помощью ПИД-регулятора 2-DOF.

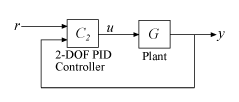
Отношение между контроллером 2-DOF выход (u) и его два входных параметров (r и y) может быть представлено или в параллельной или в стандартной форме. Две формы отличаются по параметрам, используемым, чтобы описать пропорциональное, интеграл и производные действия контроллера, как описано в следующей таблице.

Форма Формула

Форма	Формула
Параллель (`pid2` объект	$u = K_{p} (b r - y) + \frac{K_{i}}{s} (r - y) + \frac{K_{d} s}{T_{f} s + 1} (c r - y) .$ В этом представлении: _Kp = пропорциональная составляющая _Ki = усиление интегратора _Kd = производное усиление _Tf = производная фильтрует время b = вес заданного значения на пропорциональном термине c = вес заданного значения на производном термине
Стандарт (`pidstd2` объект	$u = K_{p} [(b r - y) + \frac{1}{T_{i} s} (r - y) + \frac{T_{d} s}{\frac{T_{d}}{N} s + 1} (c r - y)] .$ В этом представлении: _Kp = пропорциональная составляющая _Ti = время интегратора _Td = производное время N = производная фильтрует делитель b = вес заданного значения на пропорциональном термине c = вес заданного значения на производном термине

Параллель (pid2 объект

$u = K_{p} (b r - y) + \frac{K_{i}}{s} (r - y) + \frac{K_{d} s}{T_{f} s + 1} (c r - y) .$

В этом представлении:

_Kp = пропорциональная составляющая
_Ki = усиление интегратора
_Kd = производное усиление
_Tf = производная фильтрует время
b = вес заданного значения на пропорциональном термине
c = вес заданного значения на производном термине

Стандарт (pidstd2 объект

$u = K_{p} [(b r - y) + \frac{1}{T_{i} s} (r - y) + \frac{T_{d} s}{\frac{T_{d}}{N} s + 1} (c r - y)] .$

В этом представлении:

_Kp = пропорциональная составляющая
_Ti = время интегратора
_Td = производное время
N = производная фильтрует делитель
b = вес заданного значения на пропорциональном термине
c = вес заданного значения на производном термине

Используйте форму контроллера, которая удобна для вашего приложения. Например, если вы хотите описать интегратор и производные действия в терминах постоянных времени, используйте стандартную форму. Для примеров, показывающих, как создать параллельную форму и контроллеры стандартной формы, смотрите pid2 и pidstd2 страницы с описанием, соответственно.

Для получения информации о представлении ПИД-регуляторов в дискретное время смотрите Контроллеры Пропорциональной Интегральной Производной (PID) Дискретного времени.

Архитектуры управления 2-DOF

ПИД-регулятор 2-DOF является 2D входом, одним выходным контроллером формы C ₂ (s), как показано в следующем рисунке. Передаточная функция от каждого входа до выхода является самостоятельно ПИД-регулятором.

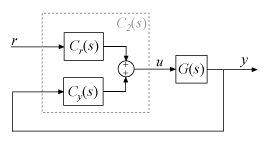
Каждый из компонентов _Cr (s) и _Cy (s) является ПИД-регулятором с различными весами на пропорциональных и производных терминах. Например, в непрерывное время, этими компонентами дают:

$\begin{array}{l} C_{r} (s) = b K_{p} + \frac{K_{i}}{s} + \frac{c K_{d} s}{T_{f} s + 1}, \\ C_{y} (s) = - [K_{p} + \frac{K_{i}}{s} + \frac{K_{d} s}{T_{f} s + 1}] . \end{array}$

Можно получить доступ к этим компонентам путем преобразования ПИД-регулятора в 2D вход, передаточную функцию с одним выходом. Например, предположите тот C2 ПИД-регулятор 2-DOF, сохраненный как a pid2 объект.

C2tf = tf(C2);
Cr = C2tf(1);
Cy = C2tf(2);

_Cr (s) является передаточной функцией от первого входа C2 к выходу. Точно так же _Cy (s) является передаточной функцией от второго входа C2 к выходу.

Предположим тот G модель динамической системы, такая как a zpk модель, представляя объект. Создайте передаточную функцию с обратной связью от r до y. Обратите внимание на то, что _Cy (s) цикл имеет положительную обратную связь по определению _Cy (s).

T = Cr*feedback(G,Cy,+1)

В качестве альтернативы используйте connect команда, чтобы создать эквивалентную систему с обратной связью непосредственно с контроллером 2-DOF C2. Для этого установите InputName и OutputName свойства G и C2.

G.InputName = 'u';
G.OutputName = 'y';
C2.Inputname = {'r','y'};
C2.OutputName = 'u';
T = connect(G,C2,'r','y');

Существуют другие настройки, в которых можно разложить ПИД-регулятор 2-DOF на компоненты SISO. Для конкретного выбора C (s) и X (s), каждая из следующих настроек эквивалентна архитектуре 2-DOF с C ₂ (s). Можно получить C (s) и X (s) для каждой из этих настроек с помощью getComponents команда.

Feedforward

В настройке прямого распространения ПИД-регулятор 2-DOF разложен на обычный ПИД-регулятор SISO, который берет сигнал ошибки в качестве его входа и контроллер прямого распространения.

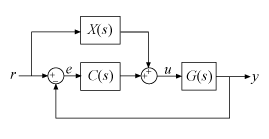
В течение непрерывного времени, параллельная форма ПИД-регулятор 2-DOF, компонентами дают:

$\begin{matrix} C (s) = K_{p} + \frac{K_{i}}{s} + \frac{K_{d} s}{T_{f} s + 1}, \\ X (s) = (b - 1) K_{p} + \frac{(c - 1) K_{d} s}{T_{f} s + 1} . \end{matrix}$

Доступ к этим компонентам использование getComponents.

[C,X] = getComponents(C2,'feedforward');

Следующая команда создает систему с обратной связью от r до y для настройки прямого распространения.

T = G*(C+X)*feedback(1,G*C);

Обратная связь

В настройке обратной связи ПИД-регулятор 2-DOF разложен на обычный ПИД-регулятор SISO и контроллер обратной связи.

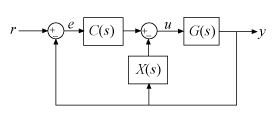
В течение непрерывного времени, параллельная форма ПИД-регулятор 2-DOF, компонентами дают:

$\begin{matrix} C (s) = b K_{p} + \frac{K_{i}}{s} + \frac{c K_{d} s}{T_{f} s + 1}, \\ X (s) = (1 - b) K_{p} + \frac{(1 - c) K_{d} s}{T_{f} s + 1} . \end{matrix}$

Доступ к этим компонентам использование getComponents.

[C,X] = getComponents(C2,'feedback');

Следующая команда создает систему с обратной связью от r до y для настройки обратной связи.

T = G*C*feedback(1,G*(C+X));

Фильтр

В настройке фильтра ПИД-регулятор 2-DOF разложен на обычный ПИД-регулятор SISO и предварительный фильтр на опорном сигнале.

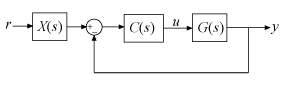
В течение непрерывного времени, параллельная форма ПИД-регулятор 2-DOF, компонентами дают:

$\begin{matrix} C (s) = K_{p} + \frac{K_{i}}{s} + \frac{K_{d} s}{T_{f} s + 1}, \\ X (s) = \frac{(b K_{p} T_{f} + c K_{d}) s^{2} + (b K_{p} + K_{i} T_{f}) s + K_{i}}{(K_{p} T_{f} + K_{d}) s^{2} + (K_{p} + K_{i} T_{f}) s + K_{i}} . \end{matrix}$

Фильтр X (s) может также быть описан как отношение: – [C _r (s)/Cy (s)].

Следующая команда создает систему с обратной связью от r до y для настройки фильтра.

T = X*feedback(G*C,1);

Для примера, иллюстрирующего разложение ПИД-регулятора 2-DOF в эти настройки, смотрите, Разлагают ПИД-регулятор 2-DOF на Компоненты SISO.

Формулы, показанные выше, принадлежат непрерывному времени, контроллерам параллельной формы. Контроллеры стандартной формы и контроллеры в дискретное время могут быть разложены на аналогичные настройки. getComponents команда работает над всеми объектами ПИД-регулятора 2-DOF.

Документация