Документация

Конструкция B-формы

Обычно, сплайн создается из некоторой информации, как значения функции и/или производные значения, или как приближенное решение некоторого обыкновенного дифференциального уравнения. Но также возможно составить сплайн с нуля путем обеспечения его последовательности узла и его содействующей последовательности к команде spmak.

Например, если вы входите

sp = spmak(1:10,3:8);

вы предоставляете универсальную последовательность узла 1:10 и содействующая последовательность 3:8. Поскольку существует 10 узлов и 6 коэффициентов, порядок должен быть 4 (= 10 – 6), i.e., вы получаете кубический сплайн. Команда

fnbrk(sp) 

распечатывает составные части B-формы этого кубического сплайна, можно следующим образом:

knots(1:n+k) 
   1 2 3 4 5 6 7 8 9 10 
coefficients(d,n) 
   3 4 5 6 7 8 
number n of coefficients 
   6 
order k 
   4 
dimension d of target 
   1

Далее, fnbrk может использоваться, чтобы предоставить каждую из этих частей отдельно.

Но точка функциональности сплайна Curve Fitting Toolbox™ - то, что не должно быть никакой потребности в вас искать эти детали. Вы просто используете sp когда аргумент к командам, которые оценивают, дифференцируйте, интегрируйте, преобразуйте или постройте сплайн, описание которого содержится в sp.

Работа со сплайнами B-формы

Следующие команды доступны для сплайна, работают. Существует spmak и fnbrk составлять сплайн и демонтировать его снова. Использование fn2fm преобразовывать от B-формы до ppform. Можно оценить, дифференцироваться, интегрировать, минимизировать, найти нули, график, совершенствовать, или выборочно экстраполировать сплайн при помощи fnval, fnder, fndir, fnint, fnmin, fnzeros, fnplt, fnrfn, и fnxtr.

Существует пять команд для генерации последовательностей узла:

Кроме того, существует:

Чтобы отобразить сплайновую кривую с данной двумерной содействующей последовательностью и универсальной последовательностью узла, используйте spcrv.

Можно также записать собственные команды конструкции сплайна, в этом случае необходимо будет знать следующее. Конструкция сплайна, удовлетворяющего некоторым условиям интерполяции или приближения обычно, требует матрицы словосочетания, т.е. матрицы, которая, в каждой строке, содержит последовательность чисел D^rB _{j, k} (τ), т.е. r th производная в τ j th B-сплайн, для всего j, для некоторого r и некоторого сайта τ. Такая матрица обеспечивается spcol. Дополнительный аргумент позволяет, чтобы эта матрица была предоставлена spcol в экономящем место сплайне почти блокируют диагональную форму или как MATLAB^® разреженная матрица. Это может питаться slvblk, команда для решения линейных систем с матрицей коэффициентов "почти блокирует диагональ". Если вы интересуетесь наблюдением как spcol и slvblk используются в этом тулбоксе, взглянули на команды spapi, spap2, и spaps.

Кроме того, существуют стандартные программы для построения кубических сплайнов. csapi и csape обеспечьте кубический сплайн interpolant на уровне узлов к определенным данным, с помощью не-узла и различных других граничных условий, соответственно. Параметрическая кубическая сплайновая кривая через данные точки обеспечивается cscvn. Кубический сплайн сглаживания создается в csaps.

Пример: приближение сплайна B-формы к кругу

Как другой простой пример,

points = .95*[0 -1 0 1;1 0 -1 0]; 
sp = spmak(-4:8,[points points]);

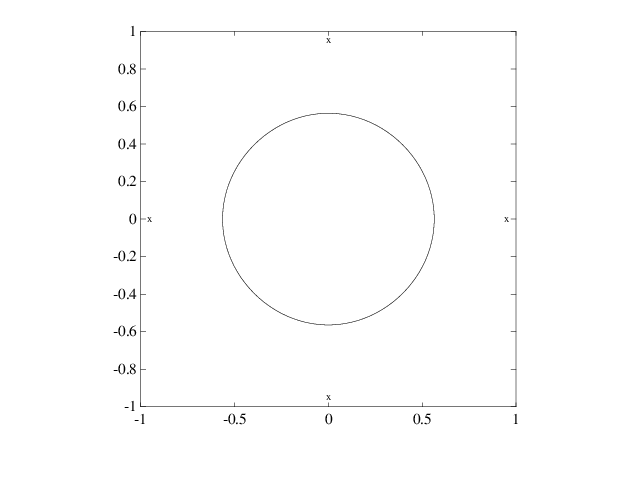
обеспечивает плоскую, биквадратную, сплайновую кривую, средняя часть которой является довольно хорошим приближением к кругу, когда график на следующей странице показывает. Это сгенерировано последующим

plot(points(1,:),points(2,:),'x'), hold on 
fnplt(sp,[0,4]), axis equal square, hold off

Вставка дополнительных контрольных точек $$\left(\pm 0.95,\pm 0.95\right)/\sqrt{1.9}$$ сделал бы визуально совершенный круг.

Вот больше деталей. Сгенерированная сплайновая кривая имеет форму Σ⁸_{j =1Bj, 5}a (: j), с-4:8 универсальная последовательность узла, и с ее контрольными точками a (: j) последовательность (0, α), (–α, 0), (0, –α), (α, 0), (0, α), (–α, 0), (0, –α), (α, 0) с α = 0.95. Только часть кривой между значениями параметров 0 и 4 на самом деле построена.

Чтобы получить чувство для того, как близко к проспекту эта часть кривой на самом деле, вычислите ее искривление без знака. Искривление κ (t) в точке кривой γ (t) = (x (t), y (t)) пространственной кривой γ может быть вычислено из формулы

в котором x, ', x ″, y', и y” являются первыми и вторыми производными кривой относительно параметра, используемого (t). Обработайте плоскую кривую как пространственную кривую в (x, y) - плоскость, следовательно получите максимум и минимум его искривления в 21 точке можно следующим образом:

t = linspace(0,4,21);zt = zeros(size(t));
dsp = fnder(sp); dspt = fnval(dsp,t); ddspt = fnval(fnder(dsp),t);
kappa = abs(dspt(1,:).*ddspt(2,:)-dspt(2,:).*ddspt(1,:))./...
   (sum(dspt.^2)).^(3/2);
[min(kappa),max(kappa)] 

ans = 
     1.6747    1.8611

Так, в то время как искривление является не совсем постоянным, это близко к 1/радиусу из круга, как вы видите от следующего вычисления:

1/norm(fnval(sp,0)) 

ans = 
     1.7864