Факторная произвольная матрица на унитарные и верхние треугольные компоненты
Математические функции / Матрицы и Линейная алгебра / Матричные Факторизации
dspfactors
Блок QR Factorization использует последовательность преобразований Домовладельца к triangularize входная матрица A. Блоковые факторы сочетание столбца M-by-N входная матрица A как
A e = QR
Вертевшийся столбцом матричный A e содержит столбцы A, переставленного, как обозначено содержимым вектора сочетания длины-N E.
Ae = A(:,E) % Equivalent MATLAB code
Блок выбирает вектор сочетания столбца E, который гарантирует, что диагональные элементы матричного R располагаются в порядке уменьшающейся величины.
Размер матриц Q и R зависит от установки параметра Output size:
Когда вы выбираете Economy для выходного размера Q является M - min (M, N) унитарная матрица, и R является min (M, N)-by-N верхняя треугольная матрица.
[Q R E] = qr(A,0) % Equivalent MATLAB code
Когда вы выбираете Full для выходного размера Q является M-by-M унитарная матрица, и R является M-by-N верхняя треугольная матрица.
[Q R E] = qr(A) % Equivalent MATLAB code
Блок обрабатывает длину-M, неориентированную на векторный вход как M-by-1 матрица.
QR-факторизация является важным инструментом для решения линейных систем уравнений из-за хороших свойств передачи ошибок и обратимости унитарных матриц:
Q –1 = Q '
где Q ' комплексное сопряженное транспонирование Q.
В отличие от LU и факторизаций Холесского, матричный A не должен быть квадратным для QR-факторизации. Однако QR-факторизация требует вдвое большего количества операций как LU-факторизации (Исключение Гаусса).
Параметр Output size блока QR-факторизации имеет две настройки: Economy и Full. Когда M-by-N входная матрица, A имеет размерности, таким образом, что M> N, размерности выходных матриц Q и R отличается в зависимости от установки параметра Output size. Если, однако, размер входной матрицы A таков, что M ≤ N, выходные матрицы, Q и R имеют те же размерности, независимо от того, установлен ли Output size в Economy или Full.
Входом с блоком QR Factorization в следующей модели является 5- 2 матричный A. Когда вы изменяете настройки параметра Output size от Economy к Full, размерности выхода, данного блоком QR Factorization также, изменяются.
Откройте модель путем ввода ex_qrfactorization_ref в MATLAB® командная строка.
Дважды кликните блок QR Factorization, установите параметр Output size на Economy, и запустите модель.
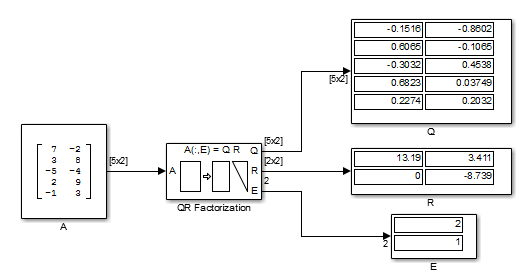
Блок QR Factorization выводит 5- 2 матричный Q и 2- 2 матричный R.
Измените параметр Output size блока QR Factorization к Full и повторно выполненный модель.
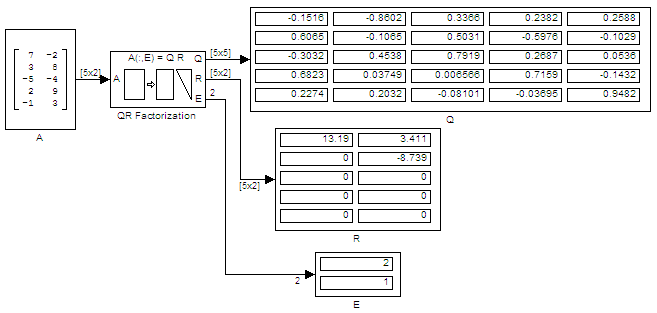
Блок QR Factorization выводит 5- 5 матричный Q и 5- 2 матричный R.
Задайте размер выходных матриц Q и R:
Economy — Когда этот выходной размер выбран, блок выводит M - min (M, N) унитарная матрица Q и min (M, N)-by-N верхняя треугольная матрица R.
Full — Когда этот выходной размер выбран, блок выводит M-by-M унитарная матрица Q и M-by-N верхняя треугольная матрица R.
Interpreted execution (значение по умолчанию)
Симулируйте модель с помощью интерпретатора MATLAB. Эта опция сокращает время запуска и имеет более быструю скорость симуляции по сравнению с Code generation.
Code generation
Симулируйте модель с помощью сгенерированного кода C. В первый раз вы запускаете симуляцию, Simulink® генерирует код С для блока. Код С снова используется для последующих симуляций, пока модель не изменяется. Эта опция требует дополнительного времени запуска, но обеспечивает более быстрые последующие симуляции.
Golub, G. H. и К. Ф. ван Лоун. Матричные Расчеты. 3-й редактор Балтимор, MD: Johns Hopkins University Press, 1996.
| Порт | Поддерживаемые типы данных |
|---|---|
Входной параметр |
|
Вывод |
|