Вычисления с фиксированной точкой

Сложение и вычитание

Сложение чисел фиксированной точки требует, чтобы двоичные точки слагаемых были выровнены. Сложение затем выполняется с помощью двоичной арифметики так, чтобы никакой номер кроме 0 или 1 не использовался.

Например, рассмотрите сложение 010010,1 (18.5) с 0110,110 (6.75):

$\begin{matrix} \begin{array}{r} \underline{\begin{matrix} 010010.1 \\ + 0110.110 \end{matrix}} \\ 011001.010 \end{array} & \begin{array}{l} (18.5) \\ (6.75) \\ (25.25) \end{array} \end{matrix}$

Вычитание фиксированной точки эквивалентно добавлению при использовании дополнительного значения two для любых отрицательных величин. В вычитании слагаемые должны быть расширены знаком, чтобы совпадать с длиной друг друга. Например, рассмотрите вычитание 0110.110 (6.75) от 010010,1 (18.5):

$\begin{matrix} \underline{\begin{matrix} 010010.100 \\ - 0110.110 \end{matrix}} & \begin{matrix} (18.5) \\ (6.75) \end{matrix} \end{matrix}$

Глобальная переменная по умолчанию fimath имеет значение 1 (TRUE) для CastBeforeSum свойство. Это бросает слагаемых к типу данных суммы перед сложением. Поэтому никакая дальнейшая перемена не необходима во время сложения, чтобы выстроить в линию двоичные точки.

Если CastBeforeSum имеет значение 0 (FALSE), слагаемые добавляются с обеспеченной полной точностью. После сложения затем квантуется сумма.

Умножение

Умножение дополнительных чисел фиксированной точки two походит на непосредственно регулярное десятичное умножение, за исключением того, что промежуточные результаты должны быть расширены знаком так, чтобы их левые стороны выровнялись, прежде чем вы добавите их вместе.

Например, рассмотрите умножение 10,11 (-1.25) с 011 (3):

Типы данных умножения

Следующие схемы показывают типы данных, используемые для умножения фиксированной точки с помощью программного обеспечения Fixed-Point Designer™. Схемы иллюстрируют различия между типами данных, используемыми для действительно-действительного, комплексно-действительного, и комплексно-комплексного умножения.

Действительно-действительное Умножение. Следующая схема показывает типы данных, используемые тулбоксом в умножении двух вещественных чисел. Программное обеспечение возвращает выходной параметр этой операции в типе данных продукта, которым управляет fimath объект ProductMode свойство.

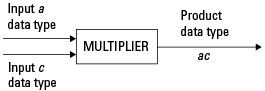
Действительно-комплексное Умножение. Следующая схема показывает типы данных, используемые тулбоксом в умножении действительного и комплексного номера фиксированной точки. Действительно-комплексное и комплексно-действительное умножение эквивалентно. Программное обеспечение возвращает выходной параметр этой операции в типе данных продукта, которым управляет fimath объект ProductMode свойство:

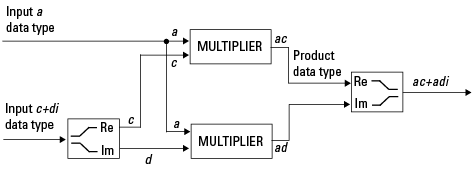
Комплексно-комплексное Умножение. Следующая схема показывает умножение двух комплексных чисел фиксированной точки. Обратите внимание на то, что программное обеспечение возвращает выходной параметр этой операции в типе данных суммы, которым управляет fimath объект SumMode свойство. Промежуточный тип данных продукта определяется fimath объект ProductMode свойство.

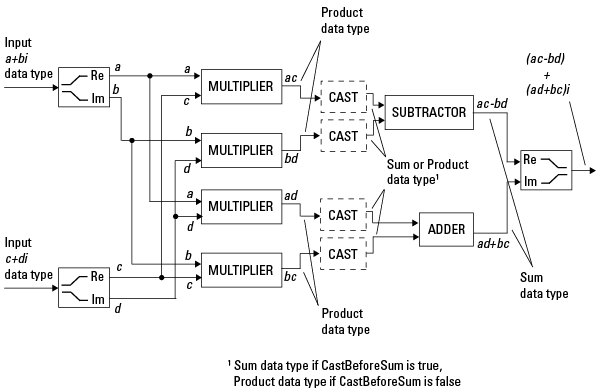
Когда fimath объект CastBeforeSum свойством является true, броски к типу данных суммы присутствуют после множителей в предыдущей схеме. В коде С это эквивалентно

acc=ac;
acc-=bd;

для вычитающего устройства, и

acc=ad;
acc+=bc;

для сумматора, где acc является аккумулятором. Когда CastBeforeSum свойством является false, броски не присутствуют, и данные остаются в типе данных продукта перед операциями вычитания и операциями сложения.

Умножение с fimath

В следующих примерах позволить

F = fimath('ProductMode','FullPrecision',...
'SumMode','FullPrecision');
T1 = numerictype('WordLength',24,'FractionLength',20);
T2 = numerictype('WordLength',16,'FractionLength',10);

Real*Real. Заметьте, что размер слова и дробная длина результата z равны сумме размеров слова и дробных длин, соответственно, множимых. Это вызвано тем, что fimath SumMode и ProductMode свойства установлены в FullPrecision:

P = fipref;
P.FimathDisplay = 'none';
x = fi(5, T1, F) 

x =
 
     5


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20

y = fi(10, T2, F) 

y =
 
    10


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10

z = x*y 

z =
 
    50


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

Real*Complex. Заметьте, что размер слова и дробная длина результата z равны сумме размеров слова и дробных длин, соответственно, множимых. Это вызвано тем, что fimath SumMode и ProductMode свойства установлены в FullPrecision:

x = fi(5,T1,F) 

x =
 
     5


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20
 
y = fi(10+2i,T2,F) 

y =
 
  10.0000 + 2.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10
 
z = x*y 

z =
 
  50.0000 +10.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 40
        FractionLength: 30

Complex*Complex. Комплексно-комплексное умножение включает сложение, а также умножение, таким образом, размер слова результата полной точности имеет еще один бит, чем сумма размеров слова множимых:

x = fi(5+6i,T1,F) 

x =
 
   5.0000 + 6.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 24
        FractionLength: 20
 
y = fi(10+2i,T2,F) 

y =
 
  10.0000 + 2.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 16
        FractionLength: 10
 
z = x*y 

z =
 
  38.0000 +70.0000i


          DataTypeMode: Fixed-point: binary point scaling
            Signedness: Signed
            WordLength: 41
        FractionLength: 30

Арифметика по модулю

Бинарная математика основана на арифметике по модулю. Арифметика по модулю использует только конечное множество чисел, перенося результаты любых вычислений, которые выходят за пределы данного, задержанного в набор.

Например, общие повседневные часы используют по модулю 12 арифметик. Числа в этой системе могут только быть 1 - 12. Поэтому в системе “часов”, 9 плюс 9 равняется 6. Это может более легко визуализироваться как круг номера:

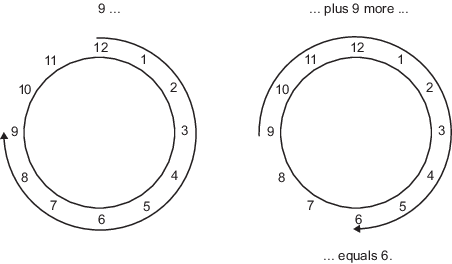
Точно так же бинарная математика может только использовать числа 0 и 1, и любые арифметические результаты, которые выходят за пределы этой области значений, перенесены “вокруг круга” или к 0 или к 1.

Дополнение Туо

Дополнение Туо является способом интерпретировать двоичное число. В дополнении two положительные числа всегда запускаются с 0, и отрицательные числа всегда запускаются с 1. Если ведущий бит дополнительного номера two 0, значение получено путем вычисления стандартного двоичного значения номера. Если ведущий бит дополнительного номера two равняется 1, значение получено путем предположения, что крайний левый бит отрицателен, и затем вычисление двоичного значения номера. Например,

$\begin{array}{l} 01 = (0 + 2^{0}) = 1 \\ 11 = ((- 2^{1}) + (2^{0})) = (- 2 + 1) = - 1 \end{array}$

Вычислить отрицание двоичного числа с помощью дополнения two,

Возьмите поразрядное дополнение до единицы, или “инвертируют биты”.
Добавьте 2^ (-FL), использование бинарной математики, где FL является дробной длиной.
Отбросьте любые биты, которые несут вне исходного размера слова.

Например, рассмотрите взятие отрицания 11 010 (-6). Во-первых, возьмите поразрядное дополнение до единицы номера или инвертируйте биты:

$11010 \to 00101$

Затем добавьте 1, перенеся все числа к 0 или 1:

$\begin{array}{l} \underline{\begin{array}{r} 00101 \\ + 1 \end{array}} \\ \begin{matrix} 00110 & (6) \end{matrix} \end{array}$

Броски

fimath объект позволяет вам задавать тип данных и масштабирование промежуточных сумм и продуктов с SumMode и ProductMode свойства. Важно иметь в виду разветвления каждого броска, когда вы устанавливаете SumMode и ProductMode свойства. В зависимости от типов данных вы выбираете, переполняетесь, и/или округление может произойти. Следующий двум примерам показывает случаи, где переполнение и округление могут произойти.

Примечание

Для большего количества примеров кастинга смотрите Бросок fi Объекты.

Кастинг от более короткого типа данных до более длительного типа данных

Рассмотрите бросок ненулевого номера, представленного 4-битным типом данных двумя дробными битами, к 8-битному типу данных с семью дробными битами:

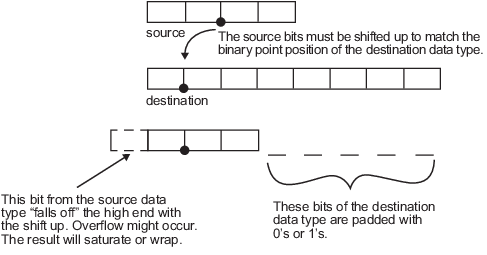
Когда схема показывает, исходные биты смещены так, чтобы двоичная точка совпадала с целевым положением двоичной точки. Самый высокий исходный бит не соответствует, таким образом, переполнение может произойти, и результат может насыщать или перенестись. Пустые биты на нижнем уровне целевого типа данных дополнены или 0 или 1's:

Если переполнение не происходит, пустые биты дополнены 0.
Если перенос происходит, пустые биты дополнены 0.
Если насыщение происходит,
- Пустые биты положительного числа дополнены 1's.
- Пустые биты отрицательного числа дополнены 0.

Вы видите, что даже с броском от более короткого типа данных до более длительного типа данных, переполнение может все еще произойти. Это может произойти, когда целочисленная длина типа исходных данных (в этом случае два) более длинна, чем целочисленная длина целевого типа данных (в этом случае один). Точно так же округление может быть необходимым, бросив от более короткого типа данных до более длительного типа данных, если целевой тип данных и масштабирование имеют меньше дробных битов, чем источник.

Кастинг от более длительного типа данных до более короткого типа данных

Рассмотрите бросок ненулевого номера, представленного 8-битным типом данных семью дробными битами, к 4-битному типу данных с двумя дробными битами:

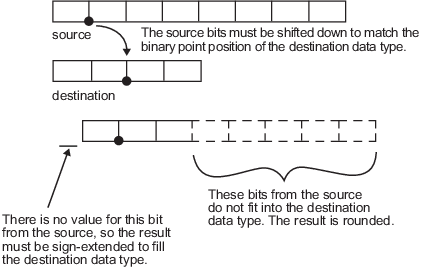
Когда схема показывает, исходные биты смещены вниз так, чтобы двоичная точка совпадала с целевым положением двоичной точки. Нет никакого значения для самого высокого бита из источника, таким образом, расширение знака используется, чтобы заполнить целочисленный фрагмент целевого типа данных. Расширение знака является сложением битов, которые имеют значение старшего значащего бита к верхнему уровню дополнительного номера two; расширение знака не изменяет значение двоичного числа. Нижняя часть пять битов источника не помещается в дробную длину места назначения. Поэтому точность может быть потеряна, когда результат округлен.

В этом случае, даже при том, что бросок от более длительного типа данных до более короткого типа данных, все целочисленные биты обеспечены. С другой стороны полная точность может быть обеспечена, даже если вы бросаете к более короткому типу данных, пока дробная длина целевого типа данных является той же длиной или дольше, чем дробная длина типа исходных данных. В этом случае, однако, биты потеряны от верхнего уровня результата, и переполнение может произойти.

Худший случай происходит, когда и целочисленная длина и дробная длина целевого типа данных короче, чем те из типа исходных данных и масштабирования. В этом случае оба переполнения и потеря точности могут произойти.

Документация