Умножение n-bit двоичного числа с двоичным числом Мбит приводит к продукту, который является до m + n биты в длине и для подписанных и для слов без знака.
Предположим, что вы хотите умножить три числа. Каждое из этих чисел представлено 5-битным словом, и у каждого есть различное единственное двоичной точкой масштабирование. Кроме того, выход ограничивается 10-битным словом с единственным двоичной точкой масштабированием 2-4. Умножение показывают в следующей модели для входных значений 5.75, 2.375, и 1.8125.
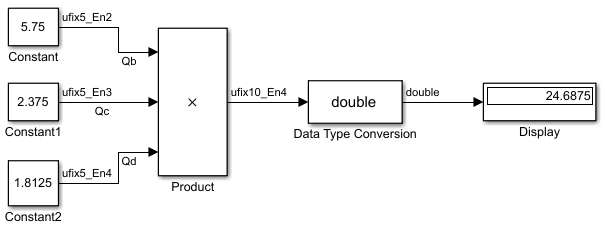
Применяя правила от предыдущего раздела, умножение выполняет эти шаги:
Первые два числа (5.75 и 2.375) умножаются:
Обратите внимание на то, что двоичная точка продукта дана суммой двоичных точек умноженных чисел.
Результат шага 1 преобразован в тип выходных данных:
Преобразования сигнала обсуждают преобразования. Обратите внимание на то, что потеря в точности одного бита происходит с получившимся значением QTemp, определенного округляющимся режимом. В данном примере раунд на пол используется. Кроме того, переполнение не произошло, но возможно для этой операции.
Результат шага 2 и третьего номера (1.8125) умножается:
Обратите внимание на то, что двоичная точка продукта дана суммой двоичных точек умноженных чисел.
Продукт преобразован в тип выходных данных:
Преобразования сигнала обсуждают преобразования. Обратите внимание на то, что потеря в точности 4 битов произошла с получившимся значением QTemp, определенного округляющимся режимом. В данном примере раунд на пол используется. Кроме того, переполнение не произошло, но возможно для этой операции.
Блоки, которые выполняют умножение, включают Product, Discrete FIR Filter и блоки Gain.