Интегральное изображение
В integral image каждый пиксель является суммированием пикселей выше и слева от него.
Чтобы проиллюстрировать, следующее показывает и изображение и его соответствующее интегральное изображение. Интегральное изображение дополнено налево и верхняя часть, чтобы допускать вычисление. Пиксельное значение в (2,1) в оригинальном изображении становится пиксельным значением (3,2) в интегральном изображении после добавления пиксельного значения выше его (2+1) и левым (3+0). Точно так же пиксель в (2,2) в оригинальном изображении со значением 4 становится пикселем в (3,3) в интегральном изображении со значением 12 после добавления пиксельного значения выше его (4+5) и добавления пикселя слева от него ((9+3).
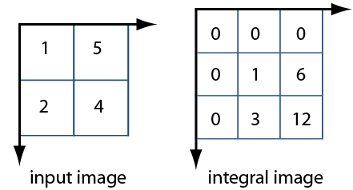
Используя интегральное изображение, можно быстро вычислить суммирование по подобластям изображений. Интегральные изображения упрощают суммирование пикселей и могут быть выполнены в постоянное время, независимо от размера окружения. Следующая фигура иллюстрирует суммирование подобласти изображения, можно использовать соответствующую область его интегрального изображения. Например, во входном изображении ниже, суммирование теневой области становится простым вычислением с помощью четырех ссылочных значений прямоугольной области в соответствующем интегральном изображении. Вычисление становится, 46 – 22 – 20 + 10 = 14. Вычисление вычитает области выше и слева от теневой области. Область перекрытия добавляется назад, чтобы компенсировать двойное вычитание.
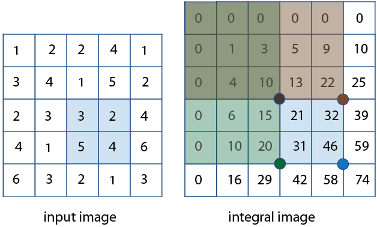
Таким образом можно вычислить суммирование в прямоугольных областях быстро, независимо от размера фильтра. Использование интегральных изображений было популяризировано алгоритмом Виолы - Джонса. Чтобы видеть полную цитату для этого алгоритма и изучить, как создать интегральное изображение, смотрите integralImage.
Смотрите также
integralImage | integralBoxFilter | integralBoxFilter3 | integralImage3