Преобразуйте матрицу ребра, чтобы скоординировать и Матрицы Лапласа
[L,XY] = unmesh(E)
[L,XY] = unmesh(E) возвращает Матрицу Лапласа L и поймайте в сети координату вершины матричный XY для M- 4 матрицы ребра E. Каждая строка матрицы ребра должна содержать координаты [x1 y1 x2 y2] из конечных точек ребра.
E | Матрица ребра M-4 E. |
L | Представление матрицы Лапласа графика. |
XY | Поймайте в сети матрицу координаты вершины. |
Возьмите простой пример квадрата с вершинами в (1,1), (1, –1), (–1, –1), и (–1,1), где связи между вершинами являются четырьмя перпендикулярными ребрами квадрата плюс одна диагональная связь между (–1, –1) и (1,1).
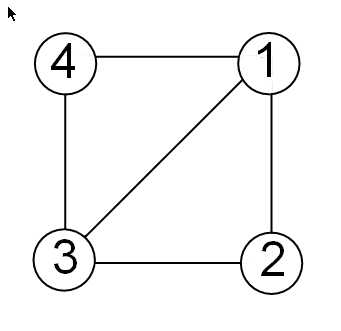
Матрица ребра E поскольку этот график:
E = [1 1 1 -1; % edge from 1 to 2 1 -1 -1 -1; % edge from 2 to 3 -1 -1 -1 1; % edge from 3 to 4 -1 -1 1 1; % edge from 3 to 1 -1 1 1 1] % edge from 4 to 1
unmesh чтобы создать Матрицу Лапласа и mesh координируют матрицу из списка ребер.[L,XY] = unmesh(E);
unmesh возвращает Матрицу Лапласа L как разреженная матрица.
L
L = (1,1) 3 (2,1) -1 (3,1) -1 (4,1) -1 (1,2) -1 (2,2) 2 (4,2) -1 (1,3) -1 (3,3) 2 (4,3) -1 (1,4) -1 (2,4) -1 (3,4) -1 (4,4) 3
L в регулярном матричном обозначении используйте full команда.full(L)
ans =
3 -1 -1 -1
-1 2 0 -1
-1 0 2 -1
-1 -1 -1 3
XY возвращает координаты углов квадрата.XY
XY =
-1 -1
-1 1
1 -1
1 1