Спроектируйте контроллер MPC для процесса бумагоделательной машины
В этом примере показано, как спроектировать прогнозирующий контроллер модели для нелинейного процесса бумагоделательной машины с помощью MPC Designer.
Модель объекта управления
Ин и др. изучил управление непротиворечивости (процент пульповых волокон в водной приостановке) и уровень жидкости в бумагоделательной машине headbox.
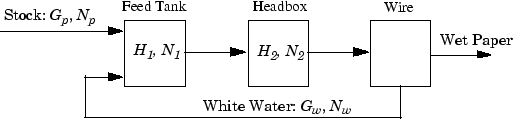
Процесс нелинеен и имеет три выходных параметров, два входных параметров, которыми управляют и два входных параметров воздействия, одни из которых измеряются для управления прямого распространения.
Модель процесса является набором обыкновенных дифференциальных уравнений (ОДУ) в билинейной форме. Состояния
H 1 — уровень жидкости Расходного бака
H 2 — уровень жидкости Headbox
N 1 — непротиворечивость Расходного бака
N 2 — непротиворечивость Headbox
Первичная цель управления состоит в том, чтобы содержать H 2 и N 2 в их заданных значениях путем корректировки переменных, которыми управляют:
Gp — Скорость потока жидкости запаса, вводящего расходный бак
Gw — Скорость потока переработанной белой воды
Непротиворечивость запаса, вводящего расходный бак, Np, является измеренным воздействием, и непротиворечивость белой воды, Nw, является неизмеренным воздействием.
Все сигналы нормированы с нулевыми номинальными установившимися значениями и сопоставимыми числовыми областями значений. Процесс является устойчивым разомкнутым контуром.
Измеренными выходными параметрами является H 2, N 1, и N 2.
Simulink® S-функция, mpc_pmmodel реализует нелинейные уравнения модели. Чтобы просмотреть эту S-функцию, введите следующее.
edit mpc_pmmodelЧтобы спроектировать контроллер для нелинейного объекта с помощью MPC Designer, необходимо сначала получить линейную модель объекта. Бумагоделательная машина headbox модель может линеаризоваться аналитически.
В MATLAB® командная строка, введите матрицы пространства состояний для линеаризовавшей модели.
A = [-1.9300 0 0 0
0.3940 -0.4260 0 0
0 0 -0.6300 0
0.8200 -0.7840 0.4130 -0.4260];
B = [1.2740 1.2740 0 0
0 0 0 0
1.3400 -0.6500 0.2030 0.4060
0 0 0 0];
C = [0 1.0000 0 0
0 0 1.0000 0
0 0 0 1.0000];
D = zeros(3,4);
Создайте модель в пространстве состояний LTI непрерывного времени.
PaperMach = ss(A,B,C,D);
Задайте имена графиков входного и выходного каналов модели.
PaperMach.InputName = {'G_p','G_w','N_p','N_w'};
PaperMach.OutputName = {'H_2','N_1','N_2'};Задайте единицы измерения времени модели.
PaperMach.TimeUnit = 'minutes';Исследуйте ответ разомкнутого контура объекта.
step(PaperMach)
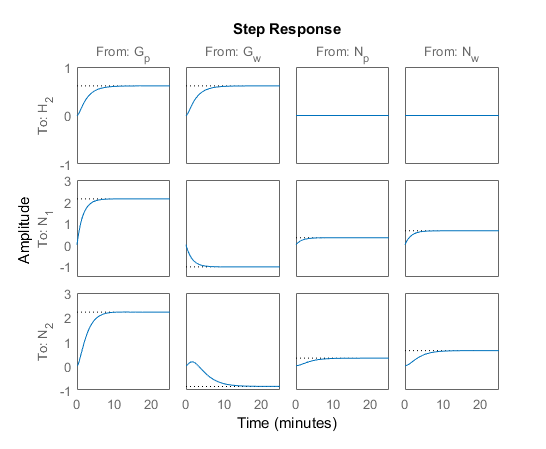
Переходной процесс показывает что:
Обе переменные, которыми управляют, Gp и Gw, влияют на все три выходных параметров.
Переменные, которыми управляют, оказывают почти идентичные влияния на H 2.
Ответ от Gw до N 2 является обратным ответом.
Эти функции мешают достигать точного, независимого управления H 2 и N 2.
Импортируйте модель объекта управления и задайте настройку сигнала
Откройте приложение MPC Designer.
mpcDesigner
В MPC Designer, на вкладке MPC Designer, в разделе Structure, нажимают MPC Structure.
В диалоговом окне Define MPC Structure By Importing выберите PaperMach модель объекта управления и присвоение ввод-вывод объекта образовывают канал к следующим типам сигнала:
Переменные, которыми управляют — Gp и Gw
Измеренное воздействие — Np
Неизмеренное воздействие — Nw
Измеренные выходные параметры — H 2, N 2, и H 2
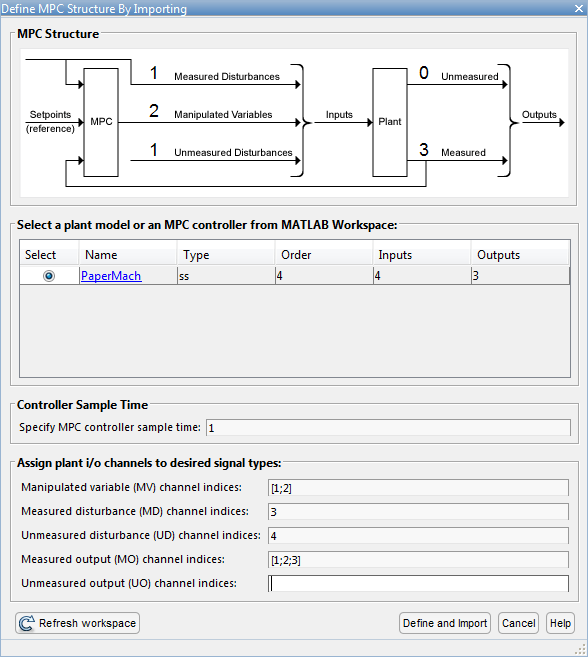
Совет
Чтобы найти правильные индексы канала, нажмите PaperMach модель Name, чтобы посмотреть дополнительные детали модели.
Нажмите Define and Import.
Приложение импортирует объект к Data Browser и создает контроллер MPC по умолчанию, использующий импортированный объект.
Задайте атрибуты канала ввода и вывода
В разделе Structure выберите I/O Attributes.
В диалоговом окне Input and Output Channel Specifications, в столбце Unit, задают модули для каждого канала. Поскольку все сигналы нормированы с нулевыми номинальными установившимися значениями, сохраняют Nominal Value и Scale Factor для каждого канала в их значениях по умолчанию.
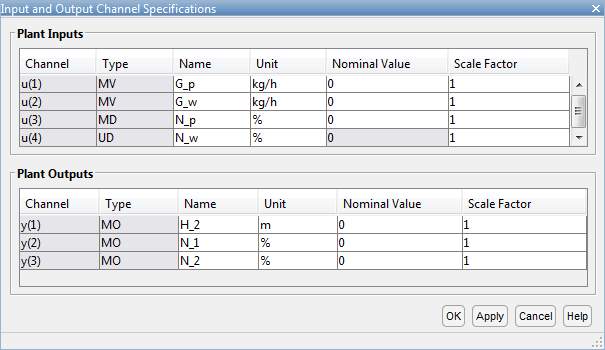
Нажмите OK, чтобы обновить атрибуты канала и закрыть диалоговое окно.
Задайте шаг расчета контроллера и горизонты
На вкладке Tuning, в разделе Horizon, сохраняют Sample time, Prediction Horizon и Control Horizon в их значениях по умолчанию.
Задайте переменные ограничения, которыми управляют,
В разделе Design нажмите Constraints.
В диалоговом окне Constraints, в разделе Input Constraints, задают ограничения значения, Min и Max, для обеих переменных, которыми управляют.
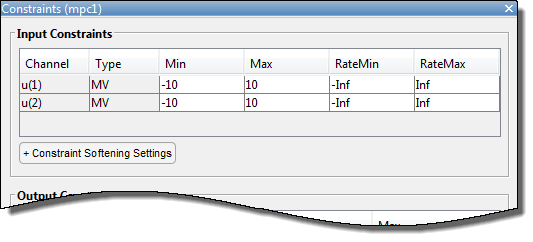
Нажмите OK.
Задайте начальные настраивающие веса
В разделе Design нажмите Weights.
В диалоговом окне Weights, в разделе Input Weights, увеличивают Rate Weight до 0.4 для обеих переменных, которыми управляют.
В разделе Output Weights задайте Weight 0 для второго выхода, N 1, и Weight 1 для других выходных параметров.
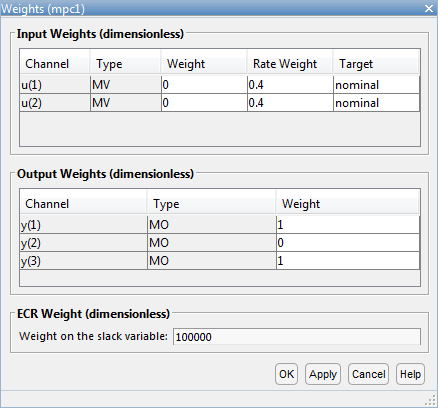
Увеличение веса уровня для переменных, которыми управляют, предотвращает чрезмерно агрессивные действия управления, приводящие к более консервативному ответу контроллера.
С тех пор существует две переменные, которыми управляют, контроллер не может управлять всеми тремя выходными параметрами полностью. Вес нуля указывает, что нет никакого заданного значения для N 1. В результате контроллер может содержать H 2 и N 2 в их соответствующих заданных значениях.
Симулируйте H 2 переходных процесса заданного значения
На вкладке MPC Designer, в разделе Scenario, нажимают Edit Scenario> scenario1.
В диалоговом окне Simulation Scenario задайте Simulation duration 30 минуты.
В таблице Reference Signals, в Signal выпадающий список, выбирают Step для первого выхода. Сохраните шаг Size в 1 и задайте шаг Time 0.
В Signal выпадающие списки для других выходных опорных сигналов выберите Constant содержать значения по их соответствующей номинальной стоимости. Контроллер игнорирует заданное значение для второго выхода, поскольку соответствующий настраивающий вес является нулем.
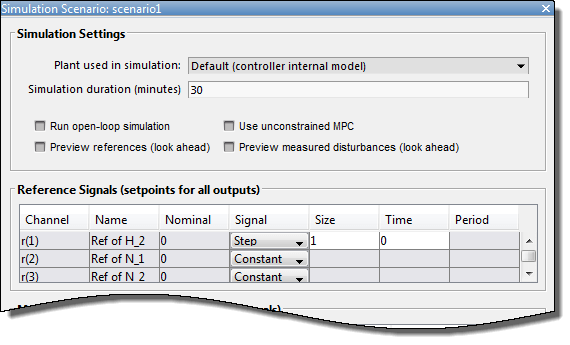
Нажмите OK.
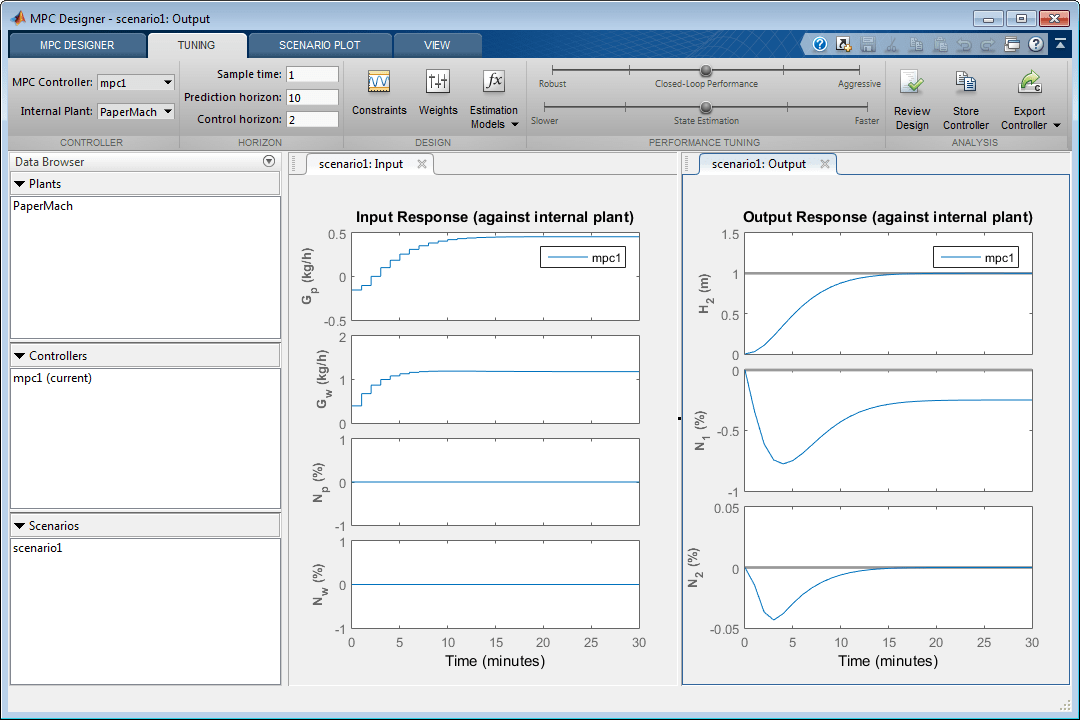
Выполнение приложения симуляция с новыми настройками сценария и обновлениями Input Response и графики Output Response.
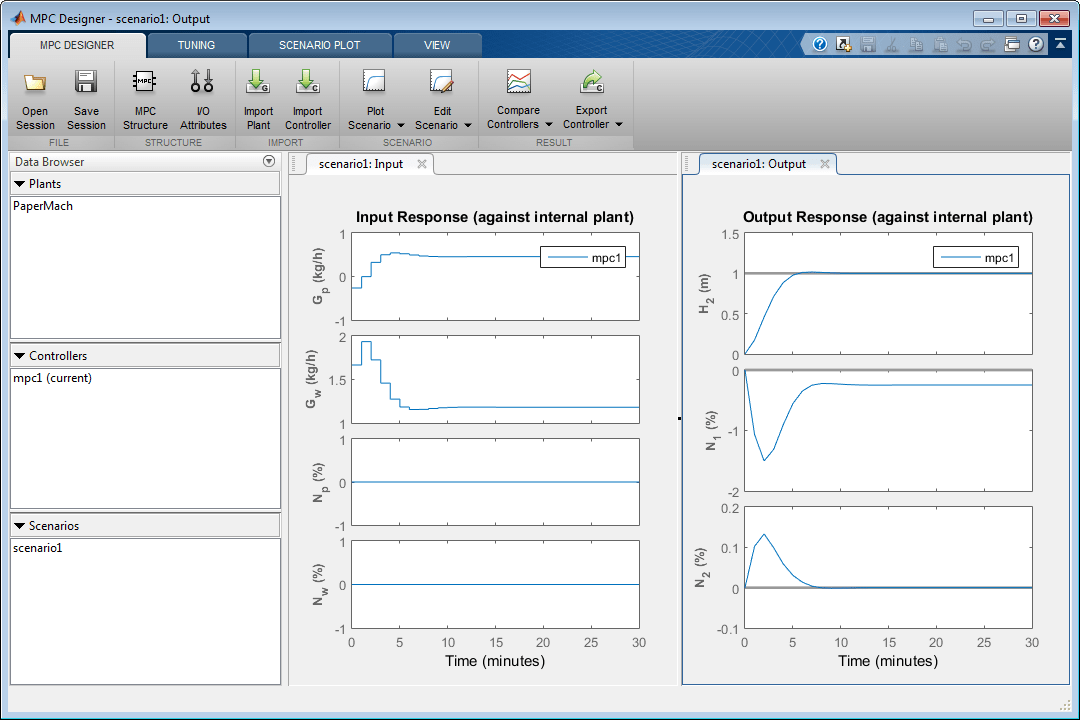
Первоначальный проект использует консервативное усилие по управлению произвести устойчивый контроллер. Время отклика для выхода H 2 составляет приблизительно 7 минут. Чтобы уменьшать это время отклика, можно уменьшить шаг расчета, уменьшать веса с плавающей ставкой, которыми управляют или уменьшать ограничения с плавающей ставкой, которыми управляют.
Поскольку настраивающийся вес для выхода N 1 является нулем, его выходной ответ показывает установившуюся ошибку приблизительно –0.25.
Настройте веса, чтобы подчеркнуть управление непротиворечивостью расходного бака
На вкладке Tuning, в разделе Design, выбирают Weights.
В диалоговом окне Weights, в разделе Output Weights, задают Weight 0.2 для первого выхода, H 2.
Контроллер уделяет больше внимания устранению ошибок в непротиворечивости расходного бака, N 2, который значительно уменьшает пиковую абсолютную погрешность. Компромисс является более длительным временем отклика приблизительно в 17 минут для уровня расходного бака, H 2.
Тестовый контроллер ответ прямого распространения на измеренные воздействия
На вкладке MPC Designer, в разделе Scenario, нажимают Plot Scenario> New Scenario.
В диалоговом окне Simulation Scenario задайте Simulation duration 30 минуты.
В таблице Measured Disturbances задайте ступенчатое изменение в измеренном воздействии, Np, с Size 1 и шаг Time 1. Сохраните все выходные заданные значения постоянными по их номинальной стоимости.
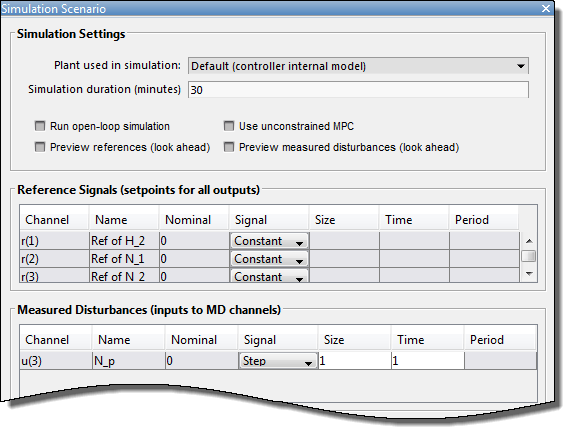
Нажмите OK, чтобы запустить симуляцию и отобразить графики отклика ввода и вывода.
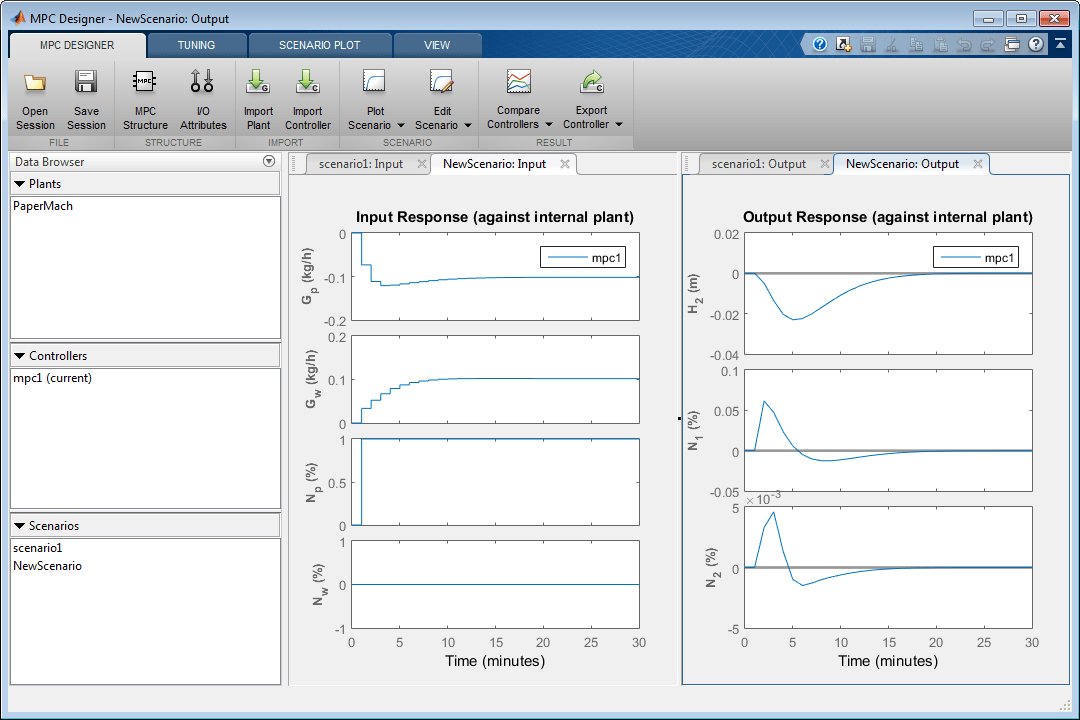
Как показано в графике NewScenario: Output, и H 2 и N 2 отклоняются мало от их заданных значений.
Экспериментируйте с предварительным просмотром сигнала
В Data Browser, в разделе Scenarios, щелкают правой кнопкой по NewScenario, и выберите Edit.
В диалоговом окне Simulation Scenario, в разделе Simulation Settings, проверяют опцию Preview measured disturbances.
Нажмите Apply.
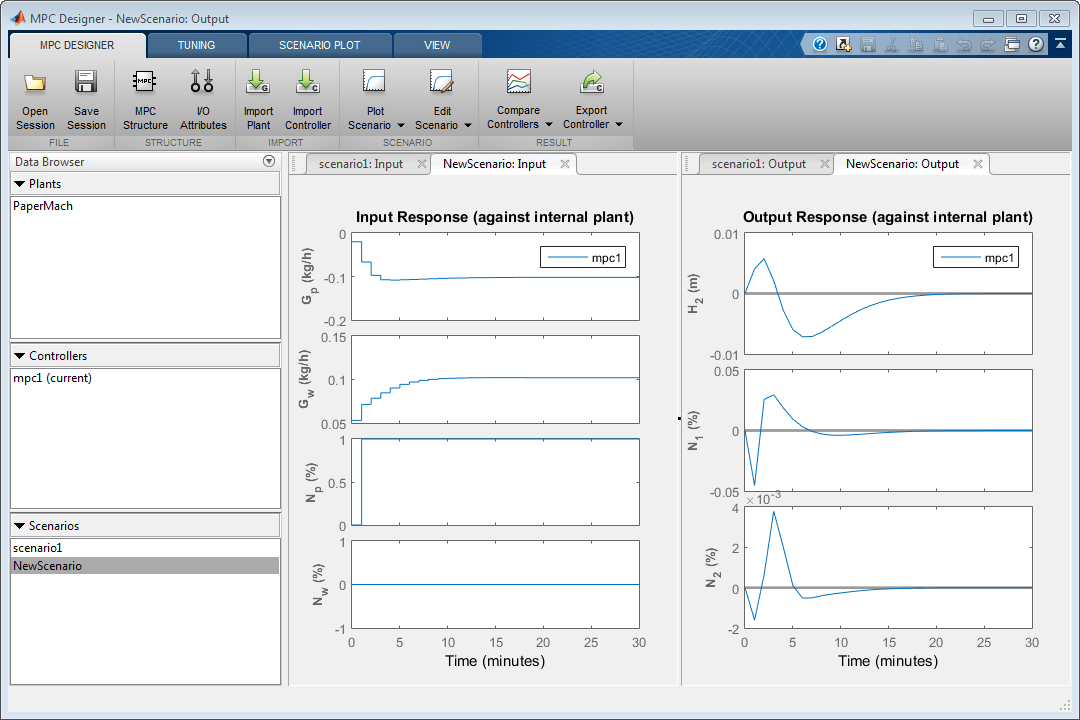
Переменные, которыми управляют, начинают изменяться, прежде чем измеренное воздействие происходит, потому что диспетчер использует известное будущее значение воздействия при вычислении его действия управления. Выходные значения воздействия также начинают изменяться, прежде чем воздействие происходит, который уменьшает величину ошибок на выходе. Однако нет никакого существенного улучшения по предыдущему результату симуляции.
В диалоговом окне Simulation Scenario очистите опцию Preview measured disturbances.
Нажмите OK.
Переименуйте сценарии
С несколькими сценариями полезно предоставить им понятные имена. В Data Browser, в разделе Scenarios, дважды кликают каждый сценарий, чтобы переименовать их как показано:
Ответная реакция тестового контроллера на неизмеренные воздействия
В Data Browser, в разделе Scenarios, щелкают правой кнопкой по Feedforward, и выберите Copy.
Дважды кликните новый сценарий и переименуйте его Feedback.
Щелкните правой кнопкой по Feedback сценарий, и выбирает Edit.
В диалоговом окне Simulation Scenario, в таблице Measured Disturbances, в Signal выпадающий список, выбирают Constant удалить измеренное воздействие.
В таблице Unmeasured Disturbances, в Signal выпадающий список, выбирают Step симулировать внезапное, выдержало неизмеренное входное воздействие.
Установите шаг Size на 1 и шаг Time к 1.
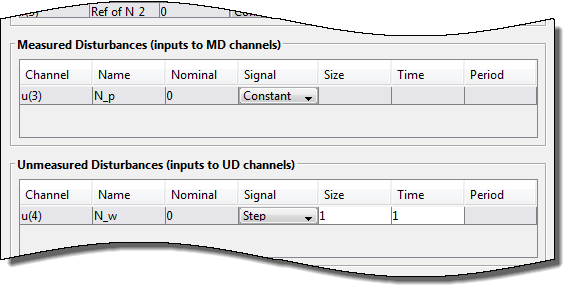
Нажмите OK, чтобы обновить настройки сценария и запустить симуляцию.
В Data Browser, в разделе Scenarios, щелкают правой кнопкой по Feedback, и выберите Plot.
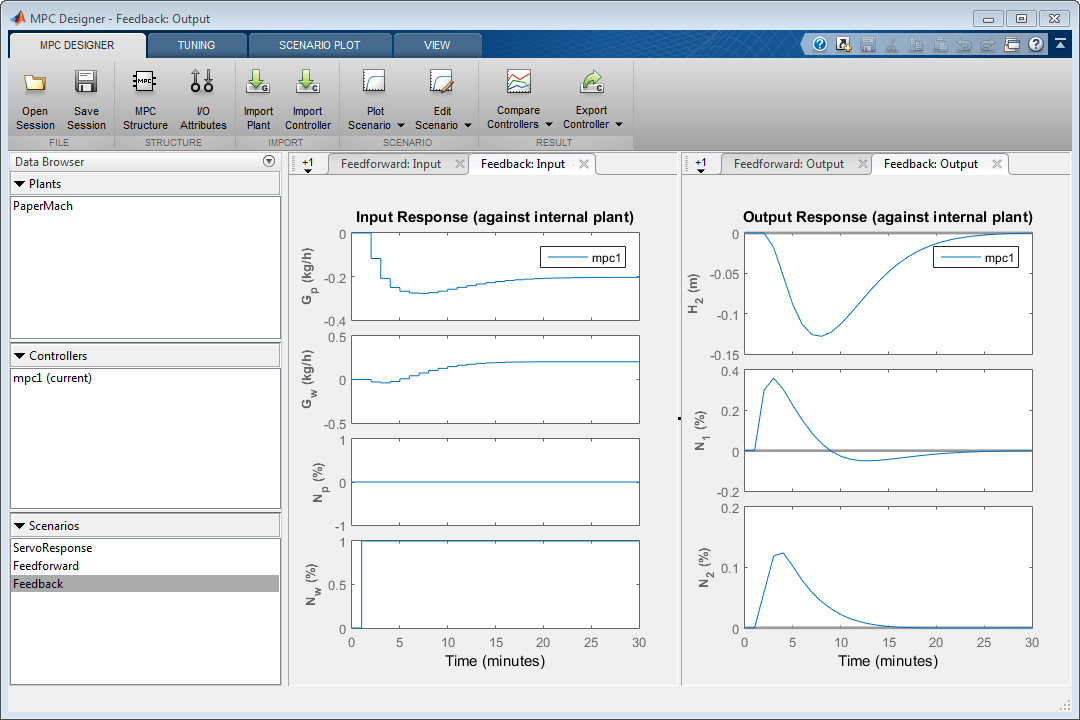
Управляемые выходные параметры, H 2 и N 2, оба показывают относительно маленькие отклонения от своих заданных значений. Время урегулирования более длинно, чем для исходного ответа сервомотора, который типичен.
На вкладке Tuning, в разделе Analysis, нажимают Review Design, чтобы проверять контроллер на потенциальную устойчивость во время выполнения или числовые проблемы.
Отчет по анализу открывается в новом окне.
Анализ отмечает два предупреждения о проектировании контроллера. Кликните по именам предупреждения, чтобы определить, указывают ли они на проблемы с проектированием контроллера.
Closed-Loop Steady-State Gains, предупреждающий, указывает, что объект больше управлял выходными параметрами, чем переменные, которыми управляют. Эта неустойчивость ввода/вывода означает, что контроллер не может устранить установившуюся ошибку для всех выходных параметров одновременно. Чтобы достигнуть цели управления отслеживания заданных значений H 2 и N 2, вы ранее устанавливаете выходной вес для N 1 обнулять. Эта установка вызывает предупреждение QP Hessian Matrix Validity, которое указывает, что один из выходных весов является нулем.
Поскольку неустойчивость ввода/вывода является известной функцией модели объекта управления бумагоделательной машины, и вы намеренно обнуляете один из выходных весов, чтобы откорректировать для неустойчивости, никакое предупреждение не указывает на проблему с проектированием контроллера.
Экспортируйте контроллер в рабочее пространство MATLAB
На вкладке MPC Designer, в разделе Result, нажимают Export Controller
.
В диалоговом окне Export Controller установите флажок в столбце Select.
В столбце Export As задайте MPC1 как имя контроллера.
Нажмите Export, чтобы сохранить копию контроллера к рабочему пространству MATLAB.
Откройте и симулируйте модель Simulink
Если у вас есть модель Simulink вашей системы, можно симулировать контроллер и подтвердить ее эффективность. Функциональность Simulink не поддерживается в MATLAB Online™.
Откройте модель.
open_system('mpc_papermachine')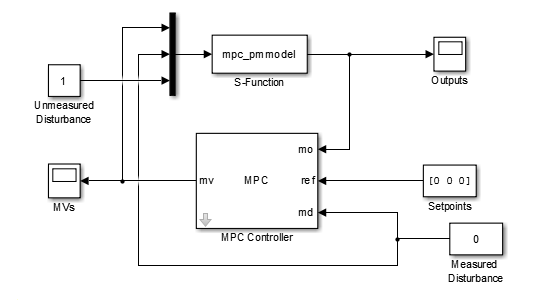
Блок MPC Controller управляет нелинейной моделью объекта управления бумагоделательной машины, которая задана с помощью S-функции mpc_pmmodel.
Модель сконфигурирована, чтобы симулировать длительное неизмеренное воздействие размера 1.
Дважды кликните блок MPC Controller.
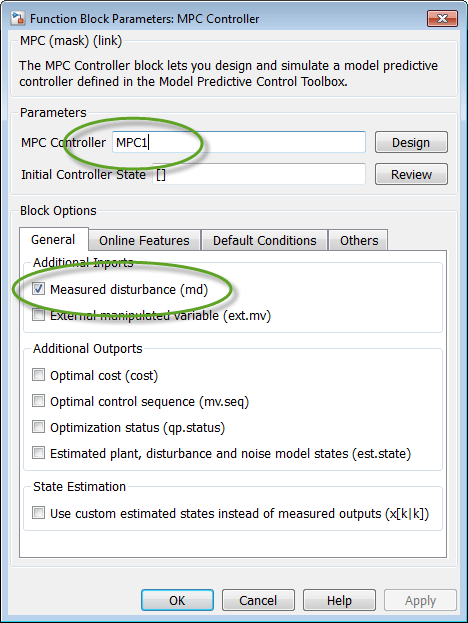
Блок MPC Controller уже сконфигурирован, чтобы использовать MPC1 контроллер, который ранее экспортировался в рабочее пространство MATLAB.
Кроме того, опция Measured disturbance выбрана, чтобы добавить md импортируйте с блоком контроллера.
Симулируйте модель.
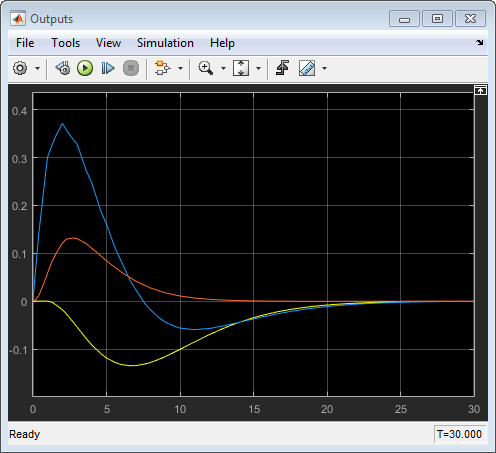
В графике Outputs ответы почти идентичны ответам от соответствующей симуляции в MPC Designer. Желтой кривой является H 2, синим является N 1, и красным является N 2.
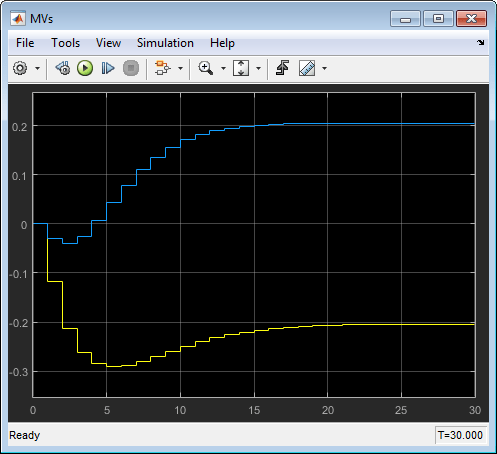
Точно так же в осциллографе MVs, переменные перемещения, которыми управляют, почти идентичны перемещениям от соответствующей симуляции в MPC Designer. Желтой кривой является Gp, и синим является Gw.
Эти результаты показывают, что нет никаких значительных ошибок предсказания из-за несоответствия между моделью линейного предсказания контроллера и нелинейным объектом. Даже увеличение неизмеренной величины воздействия на коэффициент четыре производит кривые отклика подобной формы. Однако, когда размер воздействия увеличивается далее, эффекты нелинейности становятся более явными.
Увеличьте неизмеренную величину воздействия
В окне модели Simulink дважды кликните блок Unmeasured Disturbance.
В диалоговом окне свойств Unmeasured Disturbance задайте Constant value 6.5.
Нажмите OK.
Симулируйте модель.
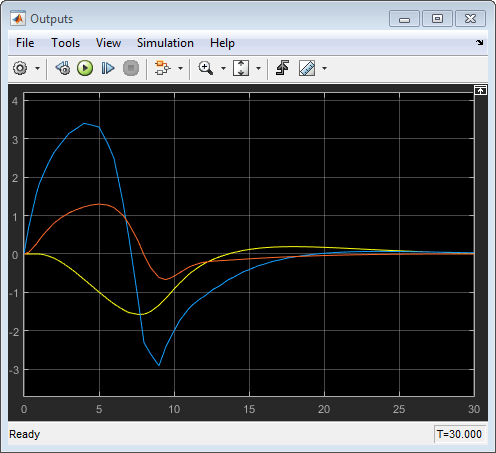
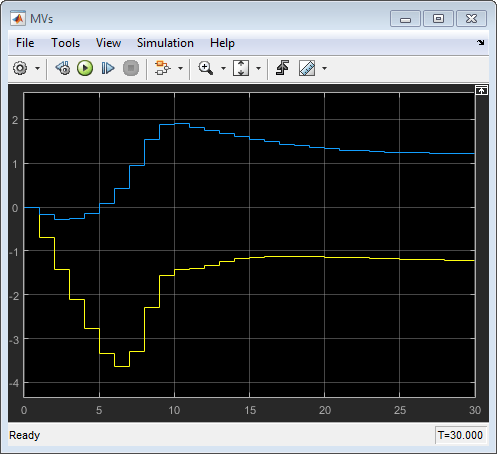
Несоответствие между моделью предсказания и объектом теперь производит выходные ответы с существенными различиями. Увеличение величины воздействия дальнейшие результаты в больших отклонениях заданного значения и насыщаемых переменных, которыми управляют.
Ссылки
[1] Ин, Y., М. Рао и И. Сун "Билинейная стратегия управления для процесса производства бумаги", Chemical Engineering Communications (1992), Издание 111, стр 13–28.