Рассеивание проблемы: приложение PDE Modeler

В этом примере показано, как решить простую задачу рассеивания, где вы вычисляете волны, отраженные квадратным объектом, освещенным инцидентными волнами, которые прибывают слева. Этот пример использует приложение PDE Modeler. Для программируемого рабочего процесса смотрите Рассеивающуюся проблему.

Для этой проблемы примите бесконечную горизонтальную мембрану, подвергнутую маленьким вертикальным смещениям U. Мембрана фиксируется на границе объекта. Носитель является гомогенным, и фазовая скорость (скорость распространения) волны, α, является постоянной. Уравнение волны

$\frac{\partial^{2} U}{\partial t^{2}} - α^{2} Δ U = 0$

Решение U является суммой инцидентного V волны и отраженного R волны:

U = V + R

Когда освещение является гармоническим вовремя, можно вычислить поле путем решения одной устойчивой задачи. Примите, что инцидентная волна является плоской волной, перемещающейся в –x направлении:

$V (x, y, t) = e^{i (- k x - ω t)} = e^{- i k x} e^{- i ω t}$

Отраженная волна может быть разложена на компоненты времени и пространственный:

$R (x, y, t) = r (x, y) e^{- i ω t}$

Теперь можно переписать уравнение волны как уравнение Гельмгольца для пространственного компонента отраженной волны с номером волны k = ω/α:

– Δr – k²r = 0

Граничным условием Дирихле для контура объекта является U = 0, или в терминах инцидента и отраженных волн, R =-V. Для гармонического временем решения и инцидентной волны, перемещающейся в –x направлении, можно записать это граничное условие можно следующим образом:

$r (x, y) = - e^{- i k x}$

Отраженные перемещения R волны, исходящие от объекта. Условие на внешнем вычислительном контуре должно позволить волнам передавать без отражения. Такие условия обычно называются, не отражаясь. Как $| \vec{x} |$ бесконечность подходов, R приблизительно удовлетворяет одностороннему уравнению волны

$\frac{\partial R}{\partial t} + α \vec{ξ} \cdot \nabla R = 0$

Это уравнение рассматривает только волны, перемещающиеся в положительный ξ - направление. Здесь, ξ является радиальным расстоянием от объекта. С гармоническим временем решением это уравнение превращается в обобщенное Нейманово граничное условие

$\vec{ξ} \cdot \nabla r = i k r$

Чтобы решить рассеивающуюся задачу в приложении PDE Modeler, выполните эти шаги:

Откройте приложение PDE Modeler при помощи pdeModeler команда.
Установите x - предел по осям [0.1 1.5] и y - предел по осям [0 1]. Для этого выберите Options> Axes Limits и установите соответствующие области значений.
Отобразить координатную сетку. Для этого:
1. Выберите Options> Grid Spacing и снимите флажки Auto.
2. Введите X-axis linear spacing как 0.1:0.05:1.5 и Y-axis linear spacing как 0:0.05:1.
3. Выберите Options> Grid.
Выровняйте новые формы к линиям сетки путем выбора Options> Snap.
Чертите квадрат со сторонами длины 0.1 и центр в [0.8 0.5]. Для этого сначала нажмите кнопку. Затем щелкните правой кнопкой по источнику и перетащите, чтобы чертить квадрат. Щелчок правой кнопкой ограничивает форму, которую вы чертите так, чтобы это был квадрат, а не прямоугольник. Если квадрат не является полным квадратом, дважды кликните его. В получившемся диалоговом окне задайте точное местоположение левого нижнего угла и длины стороны.
Вращайте квадрат 45 градусами. Для этого выберите Draw> Rotate... и войдите 45 в получившееся диалоговое окно. Вращаемый квадрат представляет освещенный объект.
Нарисуйте круг с радиусом 0,45 и центр в [0.8 0.5]. Для этого сначала нажмите кнопку. Затем щелкните правой кнопкой по источнику и перетащите, чтобы нарисовать круг. Щелчок правой кнопкой ограничивает форму, которую вы чертите так, чтобы это был круг, а не эллипс. Если круг не является совершенным модульным кругом, дважды кликните его. В получившемся диалоговом окне задайте точное центральное местоположение и радиус круга.
Смоделируйте геометрию путем ввода C1-SQ1 в поле Set formula.
Проверяйте, что режим приложения установлен в Generic Scalar.
Задайте граничные условия. Для этого переключитесь на граничный режим путем выбора Boundary> Boundary Mode. Используйте Shift +click, чтобы выбрать несколько контуров. Затем выберите Boundary> Specify Boundary Conditions.
- Для периметра круга граничное условие является Неймановым граничным условием с q = -ik, где номер волны k = 60 соответствует длине волны приблизительно 0,1 модулей. Введите g = 0 и q = -60*i.
- Для периметра квадрата граничное условие является граничным условием Дирихле:
  $r = - v (x, y) = - e^{i k \vec{a} \cdot \vec{x}}$
  В этой проблеме, потому что отраженные перемещения волны в –x направлении, граничным условием является r = –e^–ikx. Введите h = 1 и r = -exp(-i*60*x).
Задайте коэффициенты путем выбора PDE> PDE Specification или нажатия кнопки PDE на панели инструментов. Уравнение Гельмгольца является уравнением волны, но в Partial Differential Equation Toolbox™ можно обработать его как эллиптическое уравнение с =-k². Задайте c = 1, a = -3600, и f = 0.
Инициализируйте mesh путем выбора Mesh> Initialize Mesh.
Для достаточной точности вам нужны приблизительно 10 конечных элементов на длину волны. Внешняя граница должна быть расположена несколько объектных диаметров далеко от самого объекта. Совершенствуйте mesh путем выбора Mesh> Refine Mesh. Совершенствуйте mesh еще два раза, чтобы достигнуть необходимого разрешения.
Решите УЧП путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов.
Решение является комплексным. При графическом выводе решения вы получаете предупреждающее сообщение.
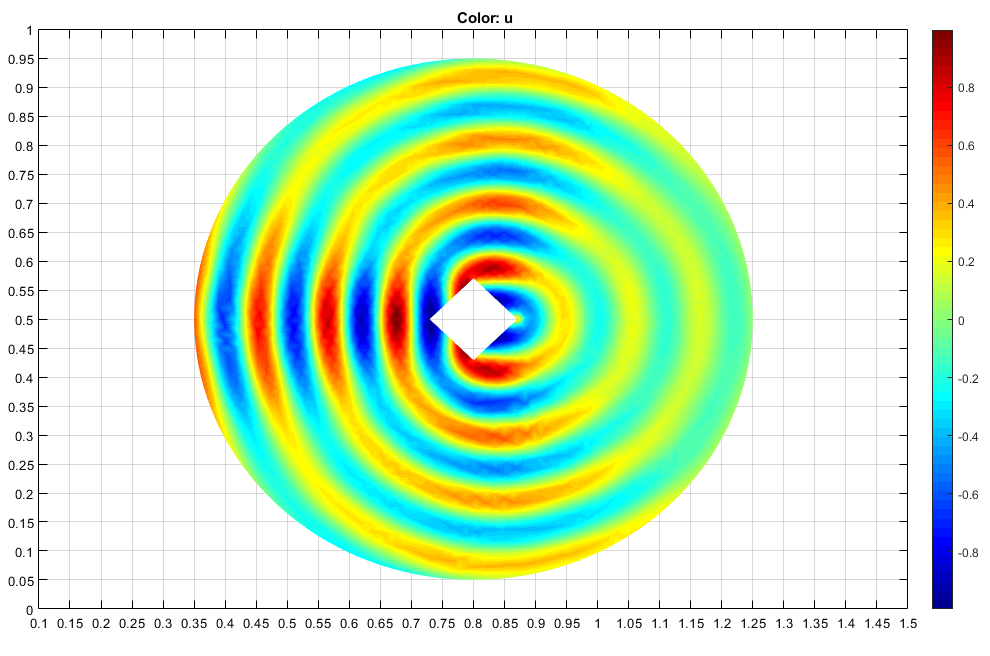
Постройте отраженные волны. Измените палитру в jet путем выбора Plot> Parameters и затем выбора jet от Colormap выпадающее меню.
Анимируйте решение для зависящего от времени уравнения волны. Для этого:
1. Экспортируйте данные о mesh и решение MATLAB^® рабочая область путем выбора Mesh> Export Mesh и Solve> Export Solution, соответственно.
2. Введите следующие команды в командное окно MATLAB.
```
figure
maxu = max(abs(u)); 
m = 10;
for j = 1:m, 
   uu = real(exp(-j*2*pi/10*sqrt(-1))*u); 
   pdeplot(p,e,t,'XYData',uu,'ColorBar','off','Mesh','off');
   colormap(jet)
   caxis([-maxu maxu]);
   axis tight
   ax = gca;
   ax.DataAspectRatio = [1 1 1]; 
   axis off
   M(:,j) = getframe; 
 end
movie(M);
```

Документация

Рассеивание проблемы: приложение PDE Modeler

Документация Partial Differential Equation Toolbox

Поддержка