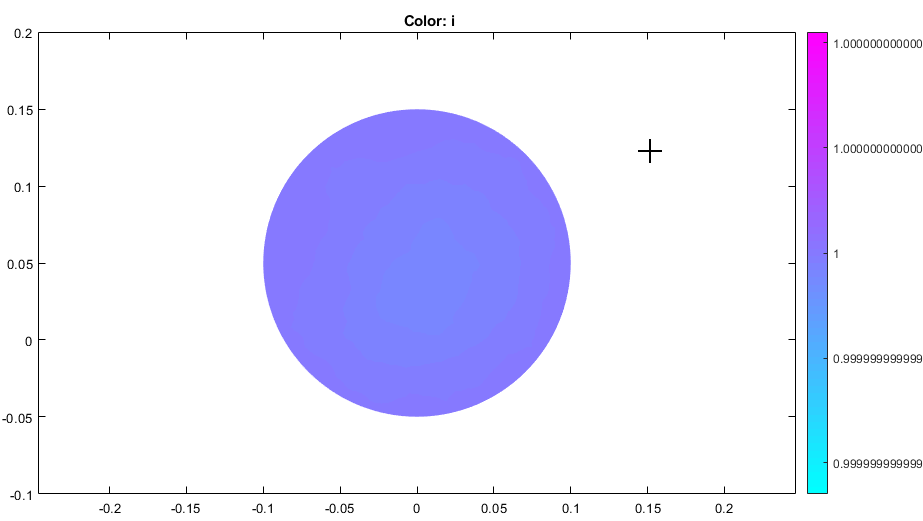
Этот пример показывает эффект кожи, когда провод с круглым сечением несет переменный ток. В твердом проводнике, таком как провод, переменный ток перемещается около поверхности провода и избегает области близко к центру провода. Этот эффект называется эффектом кожи. Пример использует приложение PDE Modeler.
Уравнение Гельмгольца
описывает распространение плоских электромагнитных волн в несовершенных диэлектриках и хороших проводниках (σ» ωε). Коэффициентом dielectricity является ε = 8.8*10-12 F/m. Проводимостью меди является σ = 57 * 106 S/m. Магнитная проницаемость меди близко к магнитной проницаемости вакуума, µ = 4π*10–7 H/m. ω2ε - термин незначителен в строчной частоте (50 Гц).
Из-за индукции, плотность тока во внутренней части проводника меньше, чем в наружной поверхности, где это установлено в JS = 1. Условием Дирихле для электрического поля является Ec = 1/σ. В этом случае аналитическое решение
Здесь,
R является радиусом провода, r является расстоянием от центральной линии, и J 0 (x) является первая Функция Бесселя нулевого порядка.
Чтобы решить эту задачу в приложении PDE Modeler, выполните эти шаги:
Нарисуйте круг с радиусом 0,1. Круг представляет сечение проводника.
pdecirc(0,0.05,0.1)
Установите x - предел по осям [-0.2 0.2] и y - предел по осям [-0.1 0.2]. Для этого выберите Options> Axes Limits и установите соответствующие области значений. Затем выберите Options> Axes Equal.
Установите режим приложения на AC Power Electromagnetics.
Задайте граничное условие Дирихле E = JS/σ = 1/σ для контура круга. Для этого:
Переключитесь на граничный режим путем выбора Boundary> Boundary Mode.
Выберите все контуры при помощи Edit> Select All.
Выберите Boundary> Specify Boundary Conditions.
Задайте h = 1 и r = 1/57E6.
Задайте коэффициенты УЧП. Для этого переключитесь на режим PDE путем выбора PDE> PDE Mode. Затем выберите PDE> PDE Specification или нажмите кнопку PDE на панели инструментов. Задайте следующие значения:
Угловая частота omega = 2*pi*50
Магнитная проницаемость mu = 4*pi*1E-7
Проводимость sigma = 57E6
Коэффициент dielectricity epsilon = 8.8E-12
Инициализируйте mesh путем выбора Mesh> Initialize Mesh.
Решите УЧП путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов.
Решение уравнения электромагнетизма мощности переменного тока является комплексным. При графическом выводе решения вы получаете предупреждающее сообщение.
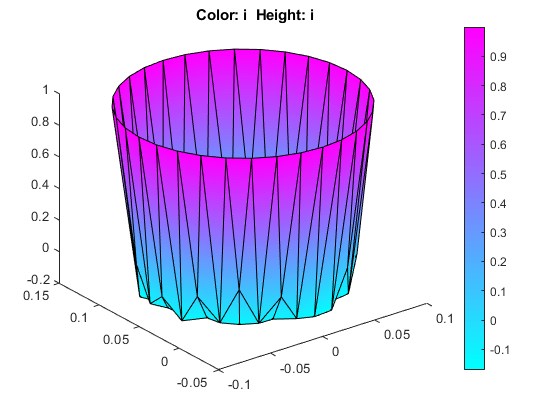
Постройте плотность тока как 3-D график. Для этого:
Выберите Plot> Parameters.
Выберите опции Height(3-D plot) и Color.
Выберите current density от Property выпадающее меню и для Color и для опций Height(3-D plot).
Выберите Show Mesh, чтобы наблюдать mesh.
Из-за эффекта кожи, плотность тока в поверхности проводника намного выше, чем во внутренней части проводника.
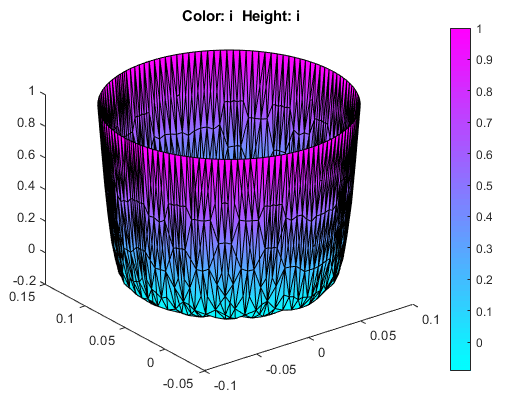
Улучшите точность решения близко к поверхности при помощи адаптивного улучшения mesh. Для этого:
Выберите Solve> Parameters.
В получившемся диалоговом окне выберите Adaptive mode.
Определите максимальные номера треугольников к Inf.
Определите максимальные номера улучшений к 1.
Выберите Worst triangles метод выбора.
Повторно вычислите решение пять раз. Каждый раз адаптивный решатель совершенствовал область с самыми большими ошибками. Количество треугольников распечатано в командной строке.
Постройте плотность тока как 3-D график.
Эти графики показывают действительную часть решения, но вектор решения является полным сложным решением. Постройте мнимую часть решения. Для этого:
Выберите Plot> Parameters.
Выберите опции Height(3-D plot) и Color.
Выберите user entry от Property выпадающее меню и для Color и для опций Height(3-D plot).
Введите imag(u) в соответствующих полях User entry.
Выберите Show Mesh, чтобы наблюдать mesh.
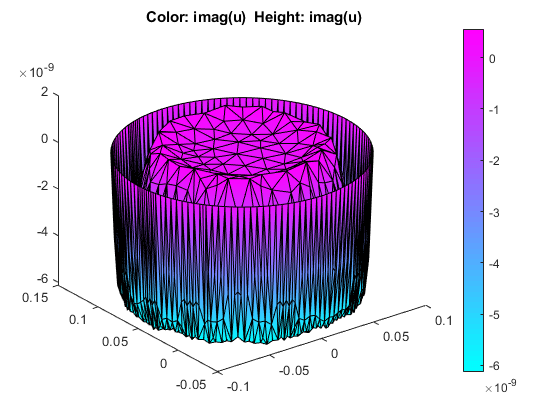
Заметьте, что эффект кожи зависит от частоты переменного тока. Когда вы увеличиваете или уменьшаете частоту, увеличения "глубины" кожи или уменьшения, соответственно. На высоких частотах только тонкий слой на поверхности провода проводит ток. В очень низких частотах (приближающиеся условия DC), почти целая площадь поперечного сечения провода проводит ток.
Найдите решение для угловых частот omega = 2*pi*1000, omega = 2*pi*50, и omega = 1E-6. Постройте действительные части решений в 2D.
Плотность тока для омеги = 2*pi*1000
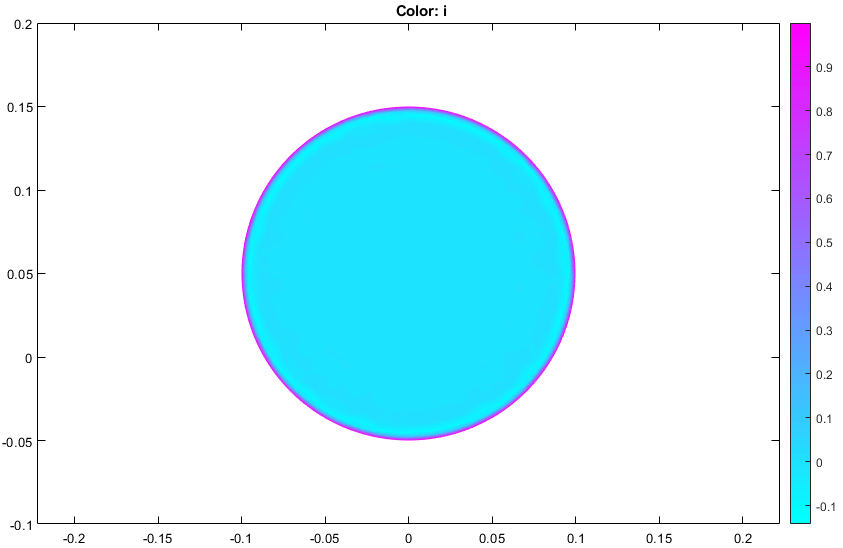
Плотность тока для омеги = 2*pi*50
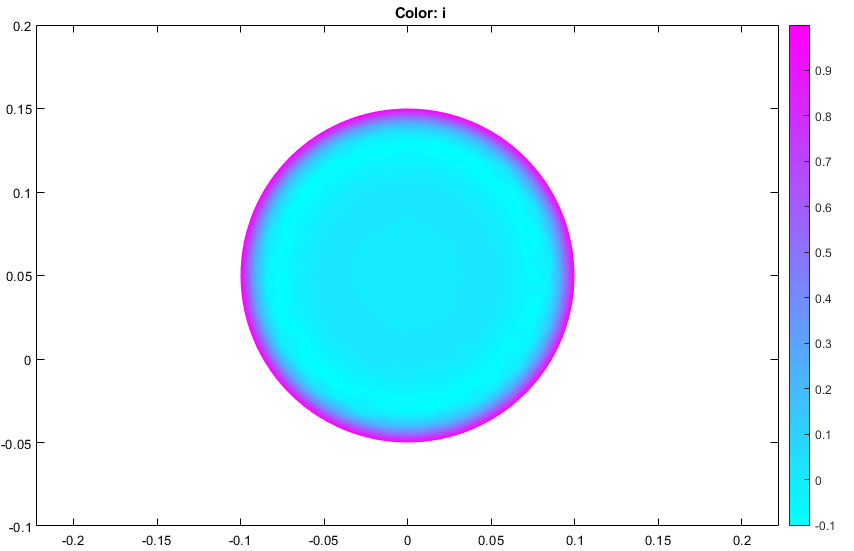
Плотность тока для омеги = 1E-6