Оценка DOA суперразрешения MUSIC

MUltiple SIgnal Classification (MUSIC) является алгоритмом определения направления с высоким разрешением на основе разложения собственного значения ковариационной матрицы датчика, наблюдаемой в массиве. MUSIC принадлежит семейству основанных на подпространстве алгоритмов определения направления.

Модель сигнала

Модель сигнала связывает полученные данные о датчике с сигналами, испускаемыми источником. Примите, что существует D некоррелированые или частично коррелированые источники сигнала, _sd(t). Данные о датчике, _xm(t), состоят из сигналов, как получено в массиве, вместе с шумом, _nm(t). Снимок состояния данных о датчике является вектором данных датчика, полученным в элементах M массива в одно время t.

$\begin{array}{l} x (t) = A s (t) + n (t) \\ s (t) = [s_{1} (t), s_{2} (t), \dots, s_{D} (t))]^{'} \\ A = [a (θ_{1}) | a (θ_{2}) | \dots | a (θ_{D})] \end{array}$

x(t) является M-by-1 вектор из полученного снимка состояния данных о датчике, которые состоят из сигналов и аддитивного шума.
A является M-by-D матрица, содержащая векторы прибытия. Вектор прибытия состоит из относительных сдвигов фазы в элементах массива плоской волны из одного источника. Каждый столбец A представляет вектор прибытия из одного из источников и зависит от направления прибытия, _θd. _θd является направлением угла падения для d th источник, и может представлять или поперечный угол для линейных матриц или азимут и угол возвышения для плоских или 3D массивов.
s(t) является D-by-1 вектор из исходных значений сигналов из источников D.
n(t) является M-by-1 вектор из значений шума датчика.

Важным количеством в любом методе подпространства является sensor covariance matrix, _Rx, выведенный из полученных данных сигнала. Когда сигналы являются некоррелироваными с шумом, ковариационная матрица датчика имеет два компонента, signal covariance matrix и noise covariance matrix.

$R_{x} = E {x x^{H}} = A R_{s} A^{H} + σ_{n}^{2} I$

где _Rs является source covariance matrix. Диагональные элементы исходной ковариационной матрицы представляют исходную степень, и недиагональные элементы представляют исходные корреляции.

$R_{s} = E {s s^{H}}$

Для некоррелированых источников или даже частично коррелируемых источников, _Rs является положительно-определенной Эрмитовой матрицей и имеет полный ранг, D, равный количеству источников.

Ковариационная матрица сигнала, _ARsA^H, M-by-M матрица, также с рангом D < M.

Предположение об алгоритме MUSIC - то, что шумовые мощности являются равными во всех датчиках и некоррелироваными между датчиками. С этим предположением шумовая ковариационная матрица становится M-by-M диагональная матрица с равными значениями по диагонали.

Поскольку истинная ковариационная матрица датчика не известна, MUSIC оценивает ковариационную матрицу датчика, _Rx, от демонстрационной ковариационной матрицы датчика. Демонстрационная ковариационная матрица датчика является в среднем несколькими снимками состояния данных о датчике

$R_{x} = \frac{1}{T} \sum_{k = 1}^{T} x (t) x {(t)}^{H},$

где T является количеством снимков состояния.

И шумовые подпространства сигнала

Поскольку _ARsA^H имеет оценивают D, он имеет D положительные действительные собственные значения и нулевые собственные значения M – D. Собственные вектора, соответствующие положительным собственным значениям, охватывают signal subspace, _{Us= [v1,...,vD]}. Собственные вектора, соответствующие нулевым собственным значениям, являются ортогональными к пробелу сигнала и охватывают null subspace, _{Un= [uD+1,...,uN]}. Векторы прибытия также принадлежат подпространству сигнала, но они - собственные вектора. Собственные вектора пустого подпространства являются ортогональными к собственным векторам подпространства сигнала. Собственные вектора пустого подпространства, _ui, удовлетворяют этому уравнению:

$A R_{s} A^{H} u_{i} = 0 \Rightarrow u^{H} A R_{s} A^{H} u_{i} = 0 \Rightarrow {(A^{H} u_{i})}^{H} R_{s} (A^{H} u_{i}) = 0 \Rightarrow A^{H} u_{i} = 0$

Поэтому векторы прибытия являются ортогональными к пустому подпространству.

Когда шум добавляется, собственные вектора ковариационной матрицы датчика с существующим шумом совпадают с бесшумной ковариационной матрицей датчика. Собственные значения увеличиваются шумовой мощностью. Позвольте _vi быть одним из исходных бесшумных собственных векторов пробела сигнала. То

$R_{x} v_{i} = A R_{s} A^{H} v_{i} + σ_{0}^{2} I v_{i} = (λ_{i} + σ_{0}^{2}) v_{i}$

показывает, что собственные значения пробела сигнала увеличиваются _σ0².

Пустые собственные вектора подпространства являются также собственными векторами _Rx. Позвольте _ui быть одним из пустых собственных векторов. То

$R_{x} u_{i} = A R_{s} A^{H} u_{i} + σ_{0}^{2} I u_{i} = σ_{0}^{2} u_{i}$

с собственными значениями _σ0² вместо нуля. Пустое подпространство становится noise subspace.

MUSIC работает путем поиска всех векторов прибытия, которые являются ортогональными к шумовому подпространству. Чтобы сделать поиск, MUSIC создает зависимое углом падения выражение степени, названное псевдоспектром MUSIC:

$P_{M U S I C} (\vec{ϕ}) = \frac{1}{a^{H} (\vec{ϕ}) U_{n} U_{n}^{H} a (\vec{ϕ})}$

Когда вектор прибытия является ортогональным к шумовому подпространству, peaks псевдоспектра бесконечен. На практике, потому что существует шум, и потому что истинная ковариационная матрица оценивается произведенной ковариационной матрицей, векторы прибытия никогда не являются точно ортогональными к шумовому подпространству. Затем углы, под которыми _PMUSIC имеет конечный peaks, являются желаемыми направлениями прибытия. Поскольку псевдоспектр может иметь больше peaks, чем существуют источники, алгоритм требует, чтобы вы задали количество источников, D, в качестве параметра. Затем алгоритм выбирает D самый большой peaks. Для универсальной линейной матрицы (ULA) пространство поиска является одномерной сеткой поперечных углов. Для плоских и 3D массивов пространство поиска является двумерной сеткой азимута и углов возвышения.

Root-MUSIC

Для ULA знаменатель в псевдоспектре является полиномом в $e^{i k d \cos φ}$ , но может также быть рассмотрен полиномом в комплексной плоскости. В этом случается, можно использовать находящие корень методы, чтобы решить для корней, _zi. Эти корни не обязательно лежат на модульном круге. Однако Root-MUSIC принимает, что корни D, самые близкие к модульному кругу, соответствуют истинным исходным направлениям. Затем можно вычислить исходные направления из фазы комплексных корней.

Пространственное сглаживание коррелированых источников

Когда некоторые исходные сигналы D коррелируются, _Rs имеет неполный ранг, означая, что он имеет меньше, чем D ненулевые собственные значения. Поэтому количество нулевых собственных значений _ARsA^H превышает номер, M – D, нулевых собственных значений для некоррелированого исходного случая. Музыкальный спектакль ухудшается, когда сигналы коррелируются, как это происходит в многопутевой среде распространения. Способ компенсировать корреляцию состоит в том, чтобы использовать пространственное сглаживание.

Spatial smoothing использует в своих интересах свойства перевода универсального массива. Рассмотрите два коррелированых сигнала, прибывающие в L - элемент ULA. Исходная ковариационная матрица, _Rs является сингулярной матрицей 2 на 2. Матрицей вектора прибытия является L-by-2 матрица

$\begin{array}{l} A_{1} = [\begin{matrix} 1 \\ e^{i k d \cos φ_{1}} \\ ⋮ \\ e^{i (L - 1) k d \cos φ_{1}} \end{matrix} \begin{matrix} 1 \\ e^{i k d \cos φ_{2}} \\ ⋮ \\ e^{i (L - 1) k d \cos φ_{2}} \end{matrix}] = [a (φ_{1}) | a (φ_{2})] \end{array}$

для сигналов, прибывающих от поперечных углов _φ1 и _φ2. Количество k является номером волны сигнала. a(φ) представляет вектор прибытия под углом φ.

Можно создать второй массив путем перевода первого массива вдоль его оси одним расстоянием элемента, d. Матрица прибытия для второго массива

$A_{2} = [\begin{matrix} e^{i k d \cos φ_{1}} \\ e^{i 2 k d \cos φ_{1}} \\ ⋮ \\ e^{i L k d \cos φ_{1}} \end{matrix} \begin{matrix} e^{i k d \cos φ_{2}} \\ e^{i 2 k d \cos φ_{2}} \\ ⋮ \\ e^{i L k d \cos φ_{2}} \end{matrix}] = [e^{i k d \cos φ_{1}} a (φ_{1}) | e^{i k d \cos φ_{2}} a (φ_{2})]$

где векторы прибытия равны исходным векторам прибытия, но умноженные на зависимый направлением сдвиг фазы. Когда вы переводите исходный массив J –1 больше раз, вы получаете копии J массива. Если вы формируете единый массив из всех этих копий, то длиной единого массива является M = L + (J – 1).

На практике вы начинаете с M - массив элемента и формируете J перекрывающиеся подрешетки. Числом элементов в каждой подрешетке является L = M – J + 1. Следующий рисунок показывает отношение между полной длиной массива, M, количества подрешеток, J, и длиной каждой подрешетки, L.

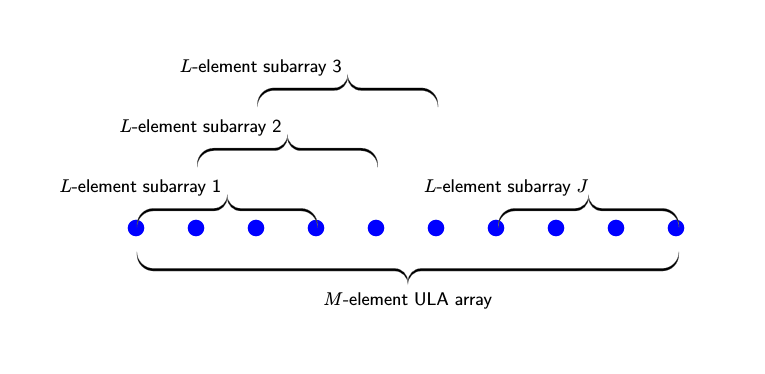
Для p th подрешетка, исходная матрица прибытия сигнала

$\begin{matrix} A_{p} = [e^{i k (p - 1) d \cos φ_{1}} a (φ_{1}) | e^{i k (p - 1) d \cos φ_{2}} a (φ_{2})] \\ = [a (φ_{1}) | a (φ_{2})] [\begin{matrix} e^{i k (p - 1) d \cos φ_{1}} & 0 \\ 0 & e^{i k (p - 1) d \cos φ_{2}} \end{matrix}] = A_{1} P^{p - 1} \\ P = [\begin{matrix} e^{i k d \cos φ_{1}} & 0 \\ 0 & e^{i k d \cos φ_{2}} \end{matrix}] . \end{matrix}$

Исходная матрица вектора прибытия постумножается на диагональную матрицу фазы.

Последний шаг составляет в среднем ковариационные матрицы сигнала по всем подрешеткам J, чтобы сформировать усредненную ковариационную матрицу сигнала, R^avg_s. Средняя ковариационная матрица сигнала зависит от сглаживавшей исходной ковариационной матрицы, R^smooth.

$\begin{array}{l} R_{s}^{a v g} = A_{1} (\frac{1}{J} \sum_{p = 1}^{J} P^{p - 1} R_{s} {(P^{p - 1})}^{H}) A_{1}^{H} = A_{1} R^{s m o o t h} A_{1}^{H} \\ R^{s m o o t h} = \frac{1}{J} \sum_{p = 1}^{J} P^{p - 1} R_{s} {(P^{p - 1})}^{H} . \end{array}$

Можно показать, что диагональные элементы сглаживавшей исходной ковариационной матрицы совпадают с диагональными элементами ковариационной матрицы первоисточника.

$R_{i i}^{s m o o t h} = \frac{1}{J} \sum_{p = 1}^{J} {(P^{p - 1})}_{i m} {(R_{s})}_{m n} {(P^{p - 1})}_{n i}^{H} = \frac{1}{J} \sum_{p = 1}^{J} R_{s} = {(R_{s})}_{i i}$

Однако недиагональные элементы уменьшаются. Фактором сокращения является диаграмма направленности J - массив элемента.

$R_{i j}^{s m o o t h} = \frac{1}{J} \sum_{p = 1}^{J} e^{i k d (p - 1) (\cos φ_{1} - \cos φ_{2})} {(R_{s})}_{i j} = \frac{1}{J} \frac{\sin (k d J (\cos φ_{1} - \cos φ_{2}))}{\sin (k d (\cos φ_{1} - \cos φ_{2}))} {(R_{s})}_{i j}$

Таким образом, можно уменьшать ухудшающийся эффект исходной корреляции путем формирования подрешеток и использования сглаживавшей ковариационной матрицы, как введено для алгоритма MUSIC. Из-за диаграммы направленности большее угловое разделение источников приводит к уменьшаемой корреляции.

Пространственное сглаживание для линейных матриц легко расширено к 2D и 3D универсальным массивам.

Документация