Метод метода расчета Моментов для металла и диэлектриков в PCB.
PCB состоит из металлической детали и диэлектрической части. Первый шаг в вычислительном решении электромагнитных проблем должен дискретизировать Уравнения Максвелла. Процесс приводит к этой матрично-векторной системе:
V— Прикладной вектор напряжения. Этот сигнал может быть напряжением, или степень применилась к антенне или инцидентному сигналу, падающему на входной порт компонента PCB.
Я — Текущий вектор, который представляет текущий на поверхности компонента PCB.
Z Матрица взаимодействия или матрица импеданса, которая имеет отношение V ко мне. Для вычисления матрицы взаимодействия эффект металлических и диэлектрических частей iof антенна PCB взят отдельно.
RF PCB Toolbox™ использует метод моментов (MoM), чтобы вычислить матрицу взаимодействия и решить системные уравнения.
Формулировка MoM разделена в три части.
Дискретизация включает формулировку от непрерывной области до дискретной области. Этот шаг называется, сцепляясь. В формулировке MoM металлическая поверхность PCB поймана в сети в треугольники, и диэлектрический объем пойман в сети в четырехгранники.
Металлы. Чтобы вычислить поверхностные токи на PCB, сначала задайте основные функции. RF PCB Toolbox использует Рао-Вилтон-Глиссона (RWG) [2] основные функции. Стрелки показывают направление электрического тока.
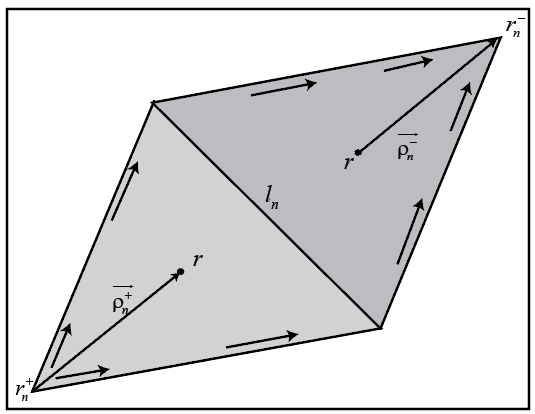
Основная функция включает пару смежных (не обязательно компланарный) треугольники и напоминает маленький пространственный диполь с линейным распределением тока. Каждый треугольник сопоставлен с положительным или отрицательным зарядом.
Для любых двух треугольных закрашенных фигур, и , наличие областей и , и совместное использование общего ребра , основная функция
— Вектор, чертивший от свободной вершины треугольника к наблюдательному посту
— Вектор, чертивший от наблюдательного поста до свободной вершины треугольника
и
Основная функция является нулем вне двух смежных треугольников и . Векторная основная функция RWG линейна и не имеет никакого потока (никакой нормальный компонент) через его контур.
Диэлектрики. Основные функции используются, чтобы представлять неизвестные количества. В случае компонента PCB неизвестные количества являются поверхностным током на металлической структуре и плотности потока из-за диэлектрического объема. RF PCB Toolbox использует Рао-Вилтон-Глиссона (RWG) [2] основные функции.
Для диэлектрического объема RF PCB Toolbox использует нулевую основную функцию ребра порядка, чтобы смоделировать плотность потока.
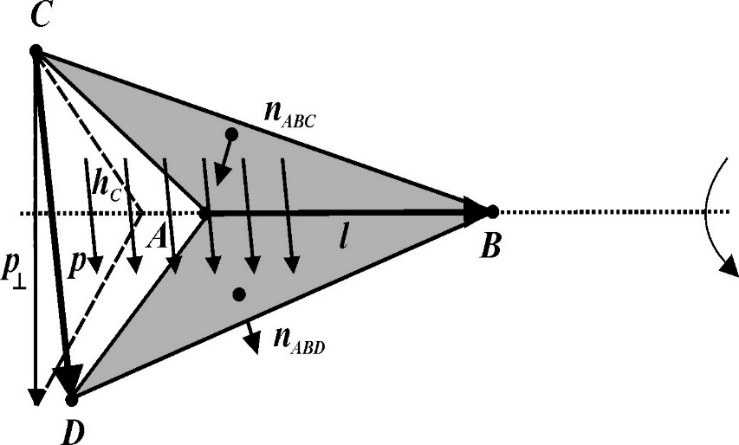
Рисунок показывает основанную на ребре основную функцию. Векторное изменение перпендикулярно основному AB ребра (или ). Вектор из CD ребра (или ) задает основную функцию. В четырехграннике основная функция является постоянным полем, данным
c коэффициент нормализации.
p вектор из ребра, задающего основную функцию.
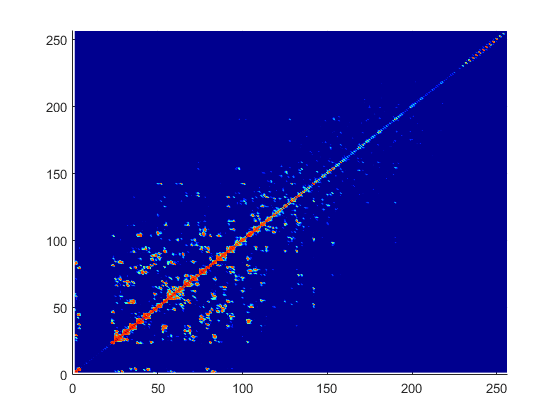
Металлы. Матрица взаимодействия является комплексной плотной симметрической матрицей. Это - квадрат N-by-N матрица, где N является количеством основных функций, то есть, количеством внутренних ребер в структуре. Типичную матрицу взаимодействия для структуры с 256 основными функциями показывают:
Чтобы заполнить матрицу взаимодействия, вычислите функцию Грина свободного пространства между всеми основными функциями на поверхности PCB. Итоговые матричные уравнения взаимодействия:
где
— Функция Грина свободного пространства
Чтобы вычислить матрицу взаимодействия, взволнуйте PCB напряжением 1 В во входном порту. Таким образом, вектор напряжения имеет нулевые значения везде кроме в питающемся ребре. Решите систему уравнений, чтобы вычислить неизвестные токи. Если вы определяете неизвестные токи, можно вычислить поле и поверхностные свойства PCB.
Диэлектрики. Матрица взаимодействия является комплексной плотной симметрической матрицей. Чтобы заполнить матрицу взаимодействия, вычислите функцию Грина свободного пространства между всеми основными функциями на поверхности PCB. Итоговые матричные уравнения взаимодействия:
ZMM – металл к металлическому взаимодействию. Для чистой металлической структуры вы только вычисляете эту симметричную квадратную матрицу.
ZDD – диэлектрик к диэлектрическому взаимодействию. Для чистых диэлектрических структур вы только вычисляете эту симметричную квадратную матрицу.
ZMD и ZDM – Эти матрицы вычисляют взаимодействие между металлом и диэлектриком. Эта матрица не является симметричной квадратной матрицей.
где
функция Грина свободного пространства.
комплексная диэлектрическая постоянная в каждом четырехграннике.
дифференциальный контраст на каждой поверхности четырехгранника.
Для составной металлической структуры необходимо вычислить все четыре матрицы.
Из матричного графика взаимодействия вы замечаете, что матрица является по диагонали доминирующей. Когда вы перемещаетесь еще дальше от диагонали, величины терминов уменьшения. Это поведение - то же самое как поведение функции Грина. Функция Грина уменьшается как расстояние между увеличениями r' и r. Поэтому важно вычислить область на диагональ и близко к диагонали точно.

Эта область на и вокруг диагонали называется соседней областью. Соседняя область задана в сфере радиуса R, где R в терминах треугольного размера. Размер треугольника является максимальным расстоянием от центра треугольника к любой из его вершин. По умолчанию R является дважды размером треугольника. Для лучшей точности схема интегрирования высшего порядка используется, чтобы вычислить интегралы. Рисунок показывает типичную матрицу взаимодействия для металлической структуры ZMM с 256 основными функциями.
Диэлектрическая матрица взаимодействия является также по диагонали доминирующей. Когда вы перемещаетесь еще дальше от диагонали, величины терминов уменьшения. Это поведение - то же самое как поведение функции Грина. Функция Грина уменьшается как расстояние между увеличениями r' и r. Поэтому важно вычислить область на диагональ и близко к диагонали точно. Для диэлектрика соседняя область основана на среднем размере четырехгранника.
По диагонали r и r' равны, и задает функцию Грина, становится сингулярным. Чтобы удалить сингулярность, экстракция выполняется на этих терминах.
Эти два интеграла на правой стороне уравнений, названных потенциальными или статическими интегралами, найдены с помощью аналитических результатов [3].
Уравнения для экстракции сингулярности ZDD матрица:
[1] Harringhton, R. F. Полевой расчет методами момента. Нью-Йорк: Макмиллан, 1968.
[2] Рао, S. M. Д. Р. Вилтон и А. В. Глиссон. “Электромагнитное рассеивание поверхностями произвольной формы”. IEEE. Сделка. Антенны и Распространение, издание AP-30, № 3, май 1982, стр 409–418.
[3] Вильтон, D. R. С. М. Рао, А. В. Глиссон, Д. Х. Шоберт, О. М. Аль-Бундак. и К. М. Батлер. “Потенциальные Интегралы для универсального и линейного исходного распределения на многоугольных и многогранных областях”. IEEE. Сделка. Антенны и Распространение. Издание AP-30, № 3, май 1984, стр 276–281.