Чисто дискретная система составлена только дискретных блоков и может быть смоделирована с помощью или фиксированного шага или решателя переменного шага. Симуляция дискретной системы требует, чтобы средство моделирования взяло шаг симуляции при каждом хите шага расчета. Для многоскоростной дискретной системы — система, чьи блоки Simulink® выборки на различных уровнях — шаги должны произойти в целочисленных множителях каждого из системных шагов расчета. В противном случае средство моделирования может пропустить ключевые переходы в состояниях системы. Размер шага, который выбирает программное обеспечение Simulink, зависит от типа решателя, который вы используете, чтобы симулировать многоскоростную систему и на основном шаге расчета.
Основной шаг расчета многоскоростной дискретной системы является самым большим двойным, которое является целочисленным делителем фактических шагов расчета системы. Например, предположите, что система имеет шаги расчета 0,25 и 0,50 секунд. Основной шаг расчета в этом случае составляет 0,25 секунды. Предположим, вместо этого, шаги расчета составляют 0,50 и 0,75 секунды. Основной шаг расчета является снова 0,25 секундами.
Важность основного шага расчета непосредственно относится, направляете ли вы программное обеспечение Simulink, чтобы использовать фиксированный шаг или переменный шаг дискретный решатель, чтобы решить вашу многоскоростную дискретную систему. Решатель фиксированного шага устанавливает размер шага симуляции, равный основному шагу расчета дискретной системы. В отличие от этого решатель переменного шага варьируется размер шага, чтобы равняться расстоянию между фактическими хитами шага расчета.
Следующая схема иллюстрирует различие между фиксированным шагом и решателем переменного шага.
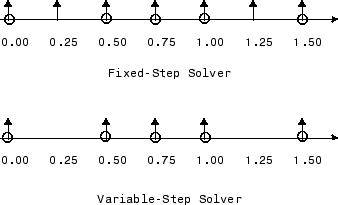
В схеме стрелки указывают на шаги симуляции, и круги представляют хиты шага расчета. Когда схема иллюстрирует, решатель переменного шага требует, чтобы меньше шагов симуляции симулировало систему, если основной шаг расчета меньше какого-либо из фактических шагов расчета симулируемой системы. С другой стороны, решатель фиксированного шага требует, чтобы меньше памяти реализовало, и быстрее, если один из системных шагов расчета является основным принципом. Это может быть преимуществом в приложениях, которые влекут за собой генерирующийся код из модели Simulink (использующий Simulink Coder™). В любом случае дискретный решатель, обеспеченный Simulink, оптимизирован для дискретных систем; однако, можно симулировать чисто дискретную систему с любым из решателей и получить эквивалентные результаты.
Рассмотрите следующий пример простой многоскоростной системы. В данном примере Шаг расчета блока DTF1 Discrete Transfer Fcn установлен в [1 0.1] [], который дает ему смещение 0.1. Шаг расчета блока DTF2 Discrete Transfer Fcn установлен в 0.7 , без смещения. Решатель установлен в переменный шаг дискретный решатель.
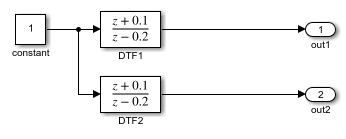
Выполнение симуляции и графический вывод выходных параметров с помощью stairs функция
set_param(bdroot,'SolverType','Variable-Step','SolverName','VariableStepDiscrete','SaveFormat','Array');
simOut = sim(bdroot,'Stoptime','3');
stairs(simOut.tout,simOut.yout,'-*','LineWidth',1.2);
xlabel('Time (t)');
ylabel('Outputs (out1,out2)');
legend('t_s = [1, 0.1]','t_s = 0.7','location','best')
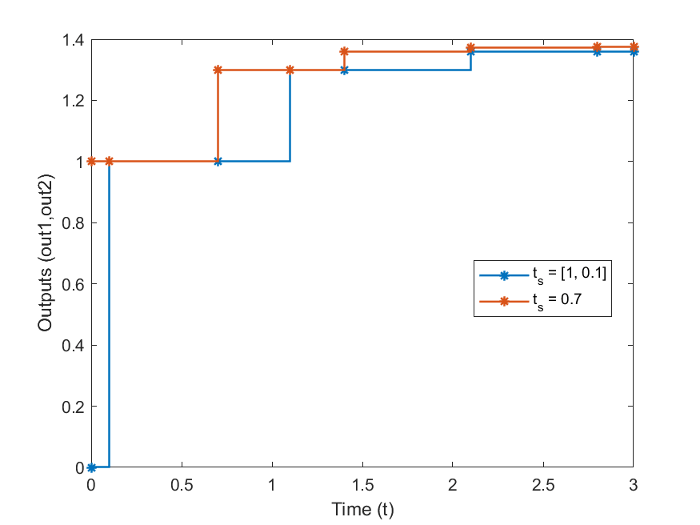
производит следующий график.
(Для получения информации о sim команда. смотрите Симуляции Запуска Программно.)
Как фигура демонстрирует, потому что блок DTF1 имеет 0.1 возместите, блок DTF1 не имеет никакого выхода до t = 0.1. Точно так же начальные условия передаточных функций являются нулем; поэтому, выход DTF1, y (1), является нулем перед этим временем.
Гибридные системы содержат и дискретные и непрерывные блоки и таким образом имеют и дискретные и непрерывные состояния. Однако решатели Simulink обрабатывают любую систему, которая имеет и непрерывные и дискретные шаги расчета как гибридную систему. Для получения информации о моделировании гибридных систем смотрите Гибридные системы Моделирования.
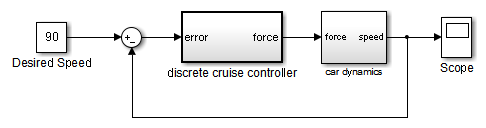
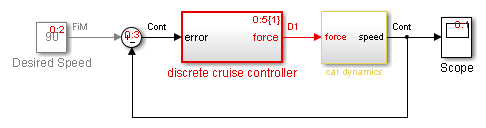
В блок-схемах термин гибрид применяется к обеим гибридным системам (смешал непрерывно-дискретные системы), и системы с несколькими шагами расчета (многоскоростные системы). Такие системы становятся желтыми в цвете, когда вы выполняете Update Diagram с Отображением Шага расчета, Colors повернул 'on'. Как пример, рассмотрите следующую модель, которая содержит атомарную подсистему, “Дискретный Контроллер Круиза” и виртуальная подсистема, “Автомобильная Динамика”. (См. ex_execution_order.)
Модель автомобиля
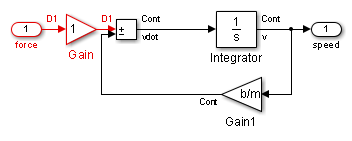
С набором опции Sample Time к All Update Diagram поворачивает виртуальную желтую подсистему, указывая, что это - гибридная подсистема. В этом случае подсистема является истинной гибридной системой, поскольку она имеет и непрерывные и дискретные шаги расчета. Как показано ниже, дискретный входной сигнал, D1, объединяется с непрерывным скоростным сигналом, v, чтобы произвести непрерывный вход для интегратора.
Модель автомобиля после Схемы Обновления
Автомобильная Подсистема Динамики после Схемы Обновления
Теперь рассмотрите многоскоростную подсистему, которая содержит три исходных блока Sine Wave, каждый из которых имеет уникальный шаг расчета — 0.2, 0.3, и 0.4, соответственно.
Многоскоростная Подсистема после Схемы Обновления
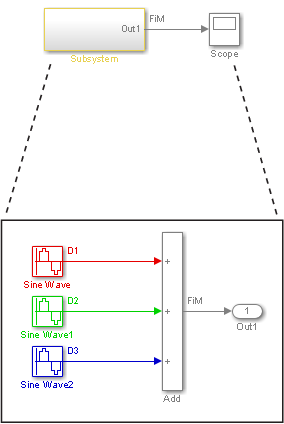
Update Diagram поворачивает подсистему, желтую, потому что подсистема содержит больше чем один шаг расчета. Как показано в блок-схеме, блоки Sine Wave имеют дискретные шаги расчета D1, D2, и D3 и выходной сигнал фиксируются на мелком шаге.
В оценке системы для нескольких шагов расчета Simulink не рассматривает ни одну константу [inf, 0] или асинхронный [–1, –n] шаги расчета. Таким образом подсистема, состоящая из одного блока, что выходное постоянное значение и один блок с дискретным шагом расчета не будут определяться как гибрид.
Гибридная аннотация и окраска очень полезны для оценки, наследовали ли подсистемы в вашей модели правильные или ожидаемые шаги расчета.
Блоки, для которых не рекомендуется шаг расчета | Просмотрите информацию о шаге расчета